快速傅里叶变换（Fast Fourier Transform, FFT）

可以在\(O(nlogn)\)的时间计算多项式乘法

或运用于计算卷积

多项式的表示

系数表示

一个次数界为\(degA=n\)的多项式\(A(x)\)可以表示为： \[ A(x)=\sum_{i=0}^{n-1}a_i x^i \] 那么两个多项式\(A(x)\)和\(B(x)\)的乘积可以表示为： \[ C(x)=A(x)B(x)=\sum_{i=0}^{2n-2}c_i x^i \\ 其中c_i=\sum_{j=0}^i a_jb_{i-j} \] 可以发现，多项式乘法其实就是对系数向量做卷积，所以FFT解决多项式乘法的同时也求出了卷积

点值表示

对于一个次数界为\(n\)的多项式\(A(x)\)，我们用\(n\)个值代入，得到\(n\)个点： \[ \{ (x_0,y_0),(x_1,y_1),\dots ,(x_{n-1},y_{n-1}) \} \] 显然这\(n\)个点能唯一确定一个次数界为\(n\)的多项式

这就为多项式的系数表示和点值表示互相转化提供了可能

点值表示可以非常方便地求多项式乘法：

对于多项式A\(\{ (x_0,y_0),(x_1,y_1),\dots ,(x_{n-1},y_{n-1}) \}\)和B\(\{ (x_0,y'_0),(x_1,y'_1),\dots ,(x_{n-1},y'_{n-1}) \}\)

其乘积为\(\{ (x_0,y_0y'_0),(x_1,y_1y'_1),\dots ,(x_{n-1},y_{n-1}y'_{n-1}) \}\)

FFT的过程

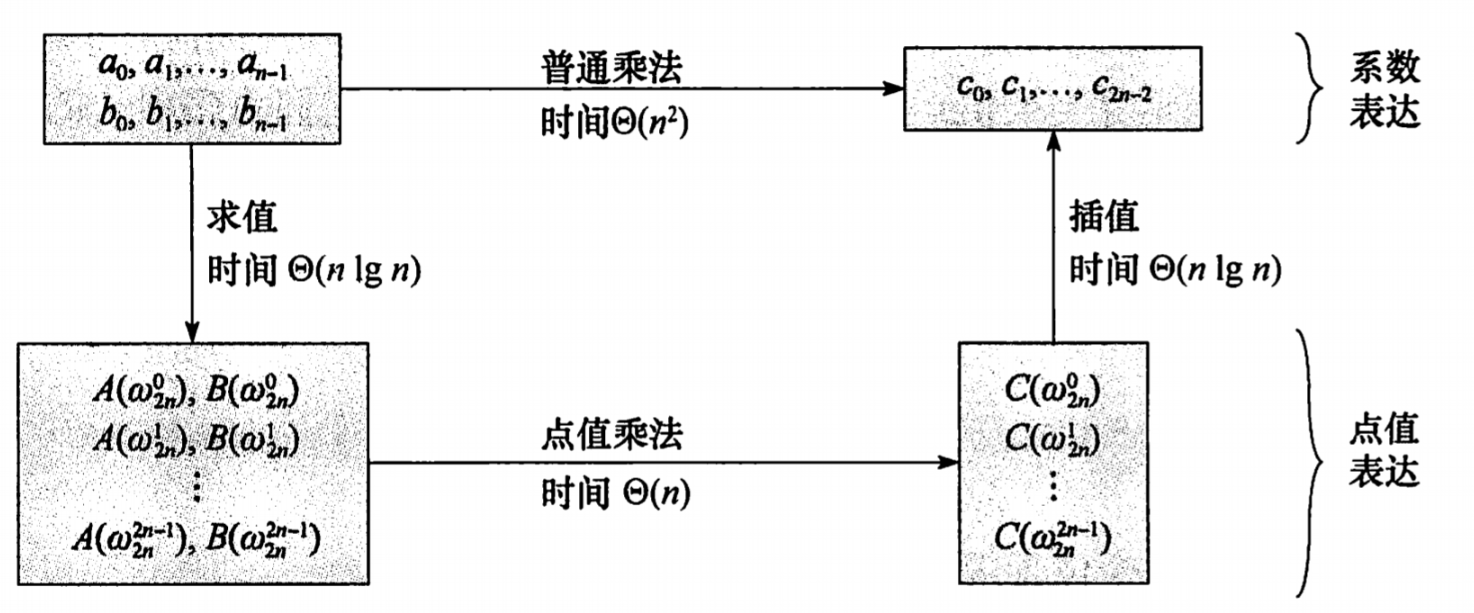
如图所示：

用DFT将多项式的系数表示转化为点值表示（求值）
用点值表示\(O(n)\)求乘积
最后用IDFT转回系数表示（插值）

DFT,IDFT

前置知识：单位复数根

n次单位复数根是满足\(\omega ^n=1\)的复数\(\omega\)

显然n次单位复数根恰好有n个

根据复数的指数形式定义： \[ e^{iu}=cos(u)+i\times sin(u) \] 以及复数单位根在复平面下的几何意义：

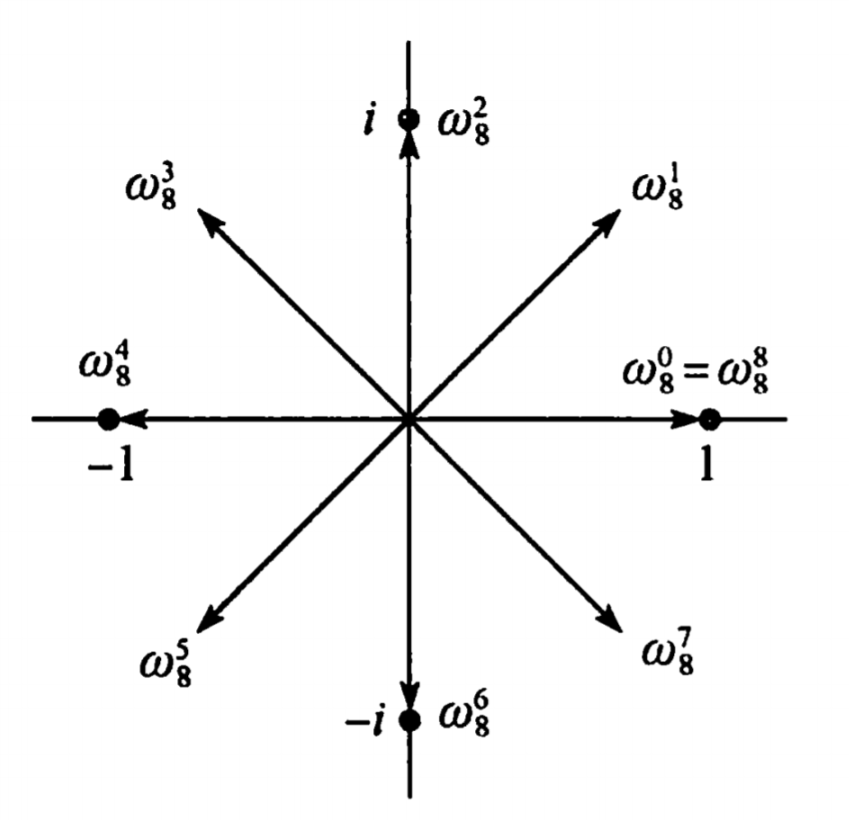
可以得到如下引理：

消去引理：对任何整数\(n\ge 0,k\ge 0\)以及\(d\gt 0\)，有\(\omega _{dn}^{dk}=\omega _n^k\)
折半引理：如果\(n\gt 0\)为整数，则n个n次单位复数根的平方构成的集合就是n/2个n/2次单位复数根的平方的集合
求和引理：对任意整数\(n\ge 1\)和不能被n整数的非负整数k，有\(\sum_{j=0}^{n-1}(\omega _n^k)^j=0\)

DFT

我们使用n个n次单位复数根\(\omega _n^i\)作为点值表示的\(x_i\)

由于单位复数根的性质，使得我们可以分治处理问题

为方便起见，以下均假设n为2的整次幂

对于多项式\(A(x)=a_0x^0+a_1x^1+a_2x^2……a_{n-1}x^{n-1}\)

我们构造两个新的多项式\(A^{[0]}(x)\)和\(A^{[1]}(x)\)： \[ A^{[0]}(x)=a_0x^0+a_2x^1+a_4x^2+……+a_{n-2}x^{n/2-1} \\ A^{[1]}(x)=a_1x^0+a_3x^1+a_5x^2+……+a_{n-1}x^{n/2-1} \]

显然有： \[ A(x)=A^{[0]}(x^2)+xA^{[1]}(x^2) \] 那么就转化成了一半规模的子问题：

考虑\(k=0,1,2……n/2-1\) \[ A(\omega _n^k)=A^{[0]}(\omega _n^{2k})+\omega _n^kA^{[1]}(\omega _n^{2k}) =A^{[0]}(\omega _{n/2}^k)+\omega _n^kA^{[1]}(\omega _{n/2}^k) \\ A(\omega _n^{k+n/2})=A^{[0]}(\omega _n^{2k+n})+\omega _n^{k+n/2}A^{[1]}(\omega _n^{2k+n}) =A^{[0]}(\omega _{n/2}^k)-\omega _n^kA^{[1]}(\omega _{n/2}^k) \]

也就是说，只需要求出\(A^{[0]}(\omega _{n/2}^k)\)和\(A^{[1]}(\omega _{n/2}^k)\)就可以求出\(A(x)\)

特殊地，当n=1时，\(A(x)\)的点值表示就是\(a_0\)

这样我们就可以递归实现DFT了，时间复杂度\(O(nlogn)\)

IDFT

把DFT写成矩阵乘法\(y=V_na\)

对矩阵\(V_n\)求逆，可以得到\(DFT^{-1}_n(y)\)： \[ a_j=\frac 1 n\sum_{k=0}^{n-1}y_k\omega_n^{-kj} \] 这和点值表示的定义非常相似： \[ y_k=\sum_{j=0}^{n-1}a_jx^j=\sum_{j=0}^{n-1}a_j\omega^{jk} \] 于是DFT的方法完全适用于IDFT

即用\(\omega^{-1}_n\)代替\(\omega_n\),计算结果每一项除以n

于是我们得到了\(O(nlogn)\)求\(DFT^{-1}_n\)的算法

迭代实现DFT

考虑递归的过程：

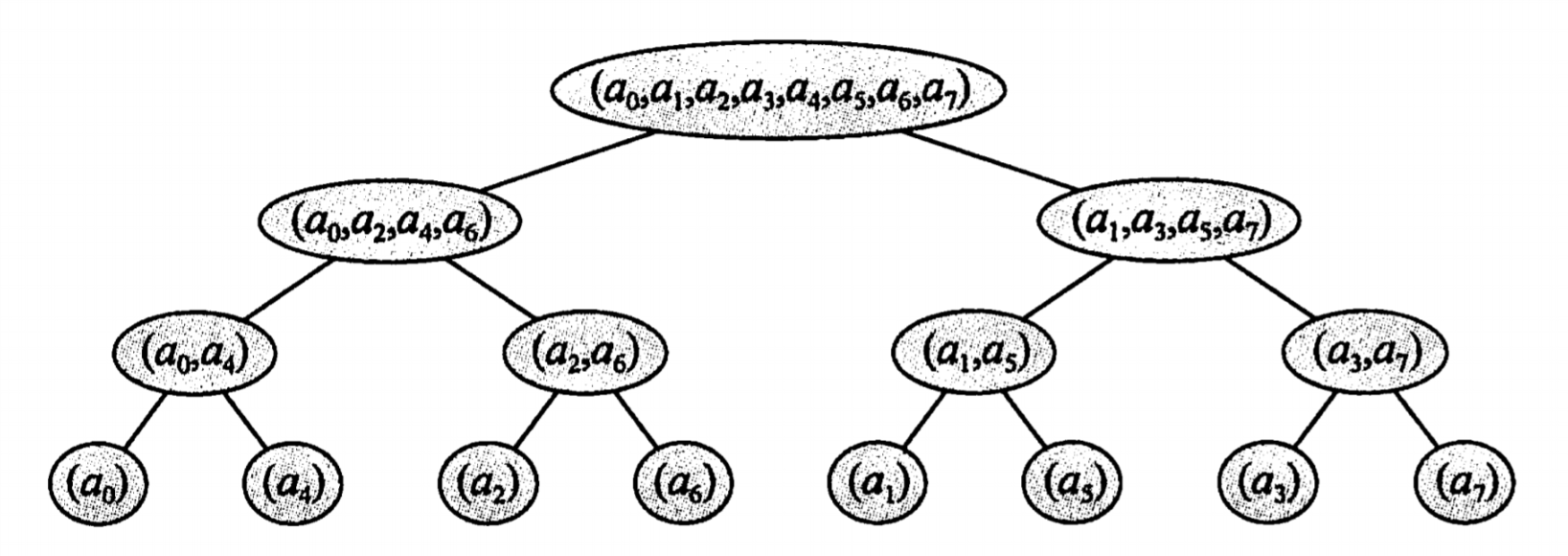
发现我们只需要知道每个元素最后在什么位置，然后一层层向上合并答案就好了

考虑按奇偶分类的过程，其实这是一棵01Trie，只是低位的优先级更高

那么每个元素的位置就是其二进制位倒过来

可以用如下代码\(O(n)\)求出每个元素最后的位置：

void get_rev(int n){
	rev[0]=0;int l=log2(n);
	for (int i=1;i<n;i++) rev[i]=(rev[i>>1]>>1)|((i&1)<<l-1);
}

模板，例题

例题：

UOJ#34

BZOJ2179

BZOJ2194

HDU1402

BZOJ3527

板子：

struct comp{
	double r,i;
	comp(double _r=0,double _i=0):r(_r),i(_i) {}
	comp operator+(const comp&b) {return comp(r+b.r,i+b.i);}
	comp operator-(const comp&b) {return comp(r-b.r,i-b.i);}
	comp operator*(const comp&b) {return comp(r*b.r-i*b.i,r*b.i+i*b.r);}
};
int rev[maxn];
inline void get_rev(int n) {for (int i=1,l=log2(n);i<n;i++) rev[i]=(rev[i>>1]>>1)|((i&1)<<l-1);}
void FFT(comp *a,int n,int d){
	for (int i=0;i<n;i++) if (rev[i]<i) swap(a[i],a[rev[i]]);
	for (int l=2;l<=n;l<<=1){
		comp wl(cos(2*PI/l),d*sin(2*PI/l));
		for (int k=0;k<n;k+=l){
			comp w(1,0),_t,_T;
			for (int j=0,tj=l>>1;j<tj;j++,w=w*wl)
			 _t=a[k+j],_T=w*a[k+j+tj],a[k+j]=_t+_T,a[k+j+tj]=_t-_T;
		}
	}
	if (d<0) for (int i=0;i<n;i++) a[i].r/=n;
}

linkfqy

A link to the past.

FFT快速傅里叶变换_remake