定义
一个有向图中,每个点有点权\(w_i\)(可负)
现在需要找到一个子图,满足:
- 对于所有边\((u,v)\),点\(u\)在子图中则\(v\)必在子图中
- 子图的点权和最大
这个子图就是最大权闭合子图
解法
我们先给出最大权闭合子图的解法,之后给出证明
最大权闭合子图可以用最小割解决:
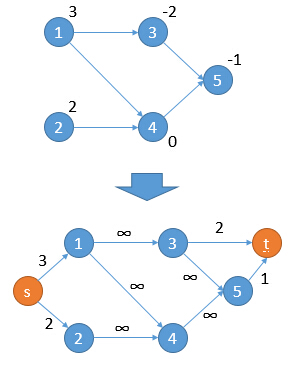
- 对于\(w_i\gt 0\)的点\(i\),连边\((S,i,w_i)\)
- 对于\(w_i\lt 0\)的点\(i\),连边\((i,T,-w_i)\)
- 对于原图边\((u,v)\),连边\((u,v,\infty)\)
答案就是所有正点权之和-最小割
证明
考虑以下两个命题:
- 最小割一定是简单割
- 简单割就是只割与\(S\)或\(T\)相连的边
- 显然成立,因为原图边都是无穷大
- 简单割与闭合子图一一对应
- 闭合子图和\(S\)构成集合\(V_S\),其余点和\(T\)构成集合\(V_T\)
- 下面是一个示例,\(V_S=\{S,2,4,5\}\):
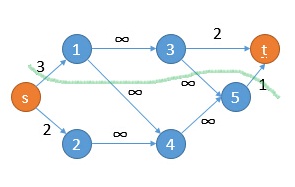
- 证明略
那么最大权闭合子图的权\(W\)=\(V_S\)中正点权和-\(V_S\)中负点权的绝对值和
最小割\(c(S,T)=\)\(V_T\)中正点权和+\(V_S\)中负点权的绝对值和
则有\(W+c(S,T)=\)所有正点权之和
就是前面说的\(W=\)所有正点权之和\(-c(S,T)\)
例题
- BZOJ1497 最大获利
- BZOJ1565 植物大战僵尸
- BZOJ4873 寿司餐厅


