Python实现插值

插值：求一函数\(f(x)\)使其穿过给定的所有数据点\((x_i,y_i)\)

在数据分析中很有用

拉格朗日插值（Lagrange）

拉格朗日插值的\(f(x)\)为\(n-1\)次多项式，\(n\)为数据点个数

可以证明，任意\(n\)个数据点的\(n-1\)次插值函数存在且唯一

具体来说， \[ f(x)=\sum_{i=0}^n l_i(x)y_i \\ l_i(x)=\prod_{j=0,j\neq i}^n \frac {x-x_j} {x_i-x_j} \] 由此公式容易用Python实现拉格朗日插值

但是一次性将所有数据点进行插值，次数过高，不仅复杂度高，误差也大，因此常进行分段插值，即用分段函数表示\(f(x)\)

样条插值（spline）

单纯的分段插值得到的函数性质往往不够好（光滑性）

对于划分：\(\Delta:a=x_0<x_1<\dots<x_n=b\)，\(m\)阶样条插值函数需要满足：

• 在每个小区间\([x_i,x_{i+1}](i=0,1,\dots,n-1)\)上是\(m\)次多项式
• 在区间\([a,b]\)上具有\(m-1\)阶导数

显然阶梯插值为0阶样条插值，折线插值为1阶样条插值

一般直接使用scipy.interpolate实现的样条插值

scipy.interpolate求解插值问题

一维插值（interp1d）

interp1d(x,y,kind='linear')

前两个参数为数据点向量，kind指定插值方法：

kind	说明
'next','previous'	阶梯插值，值为最近的前/后一个\(y_i\)
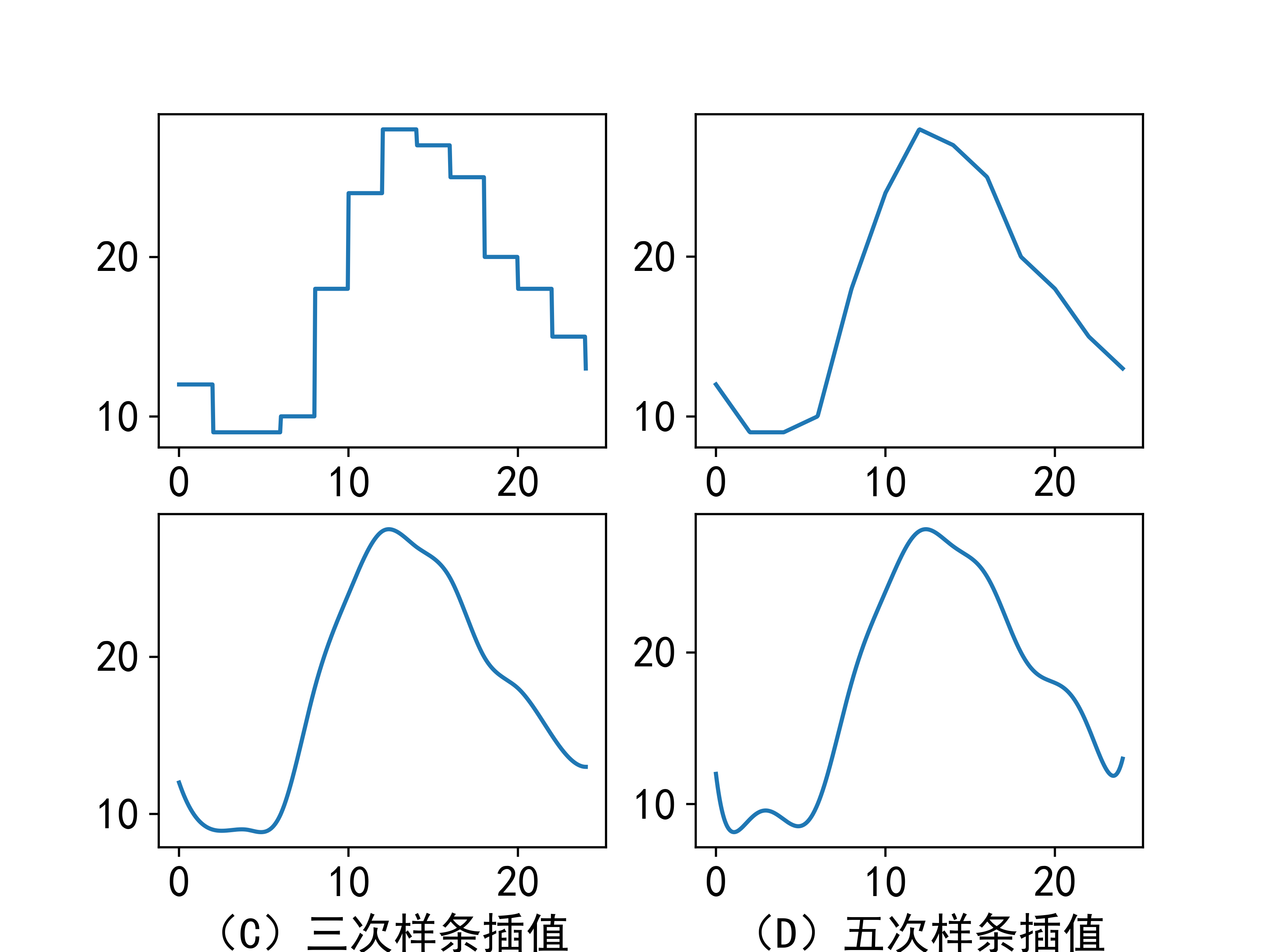
'zero', 'linear', 'quadratic', 'cubic'	0，1，2，3阶样条插值
0,1,2,3,5,...	用int指定样条插值的阶数，3以上只能为奇数

返回一个插值函数，可以传入\(x\)返回\(f(x)\)，也可以传入\(\vec x\)返回\(f(\vec x)\)

示例：

import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import interp1d
x = np.arange(0, 25, 2)
y = np.array([12, 9, 9, 10, 18, 24, 28, 27, 25, 20, 18, 15, 13])
xnew = np.linspace(0, 24, 500)
f0 = interp1d(x, y, 0)  # 'zero'
y0 = f0(xnew)
f1 = interp1d(x, y)
y1 = f1(xnew)
f3 = interp1d(x, y, 'cubic')
y3 = f3(xnew)
f5 = interp1d(x, y, 5)
y5 = f5(xnew)
plt.rc('font', size=16)
plt.rc('font', family='SimHei')
plt.subplot(221), plt.plot(xnew, y0), plt.xlabel("（A）分段阶梯插值")
plt.subplot(222), plt.plot(xnew, y1), plt.xlabel("（B）分段线性插值")
plt.subplot(223), plt.plot(xnew, y3), plt.xlabel("（C）三次样条插值")
plt.subplot(224), plt.plot(xnew, y5), plt.xlabel("（D）五次样条插值")
plt.savefig("interp1d.png", dpi=500), plt.show()

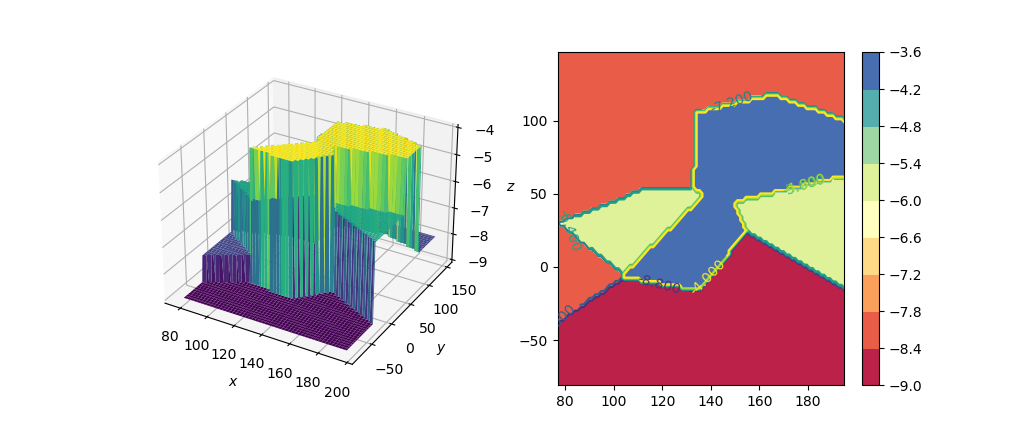
二维插值（interp2d）

interp2d(x,y,z,kind='linear')接受网格分布的数据点进行插值

x，y为坐标向量，z为数据矩阵

返回一个插值函数，输入x，y向量即可获得数据矩阵

from IPython.core.pylabtools import figsize
import matplotlib.pyplot as plt
import numpy as np
from scipy.interpolate import interp2d
from mpl_toolkits import mplot3d
z = np.loadtxt("data.txt")
x = np.arange(0, 1500, 100)
y = np.arange(1200, -100, -100)  # 文件里的y是倒序输入的
f = interp2d(x, y, z, kind='cubic')
xn = np.linspace(0, 1400, 141)
yn = np.linspace(0, 1200, 121)
zn = f(xn, yn)
plt.rc('font', size=16)
plt.subplot(1, 2, 1)
plt.contour(xn, yn, zn)
plt.xlabel('$x$'), plt.ylabel('$y$', rotation=90)
ax = plt.subplot(1, 2, 2, projection='3d')
X, Y = np.meshgrid(xn, yn)
ax.plot_surface(X, Y, zn, cmap='viridis')
ax.set_xlabel('$x$'), ax.set_ylabel('$y$'), ax.set_zlabel('$z$')
plt.savefig('interp2d.png', dpi=500), plt.show()

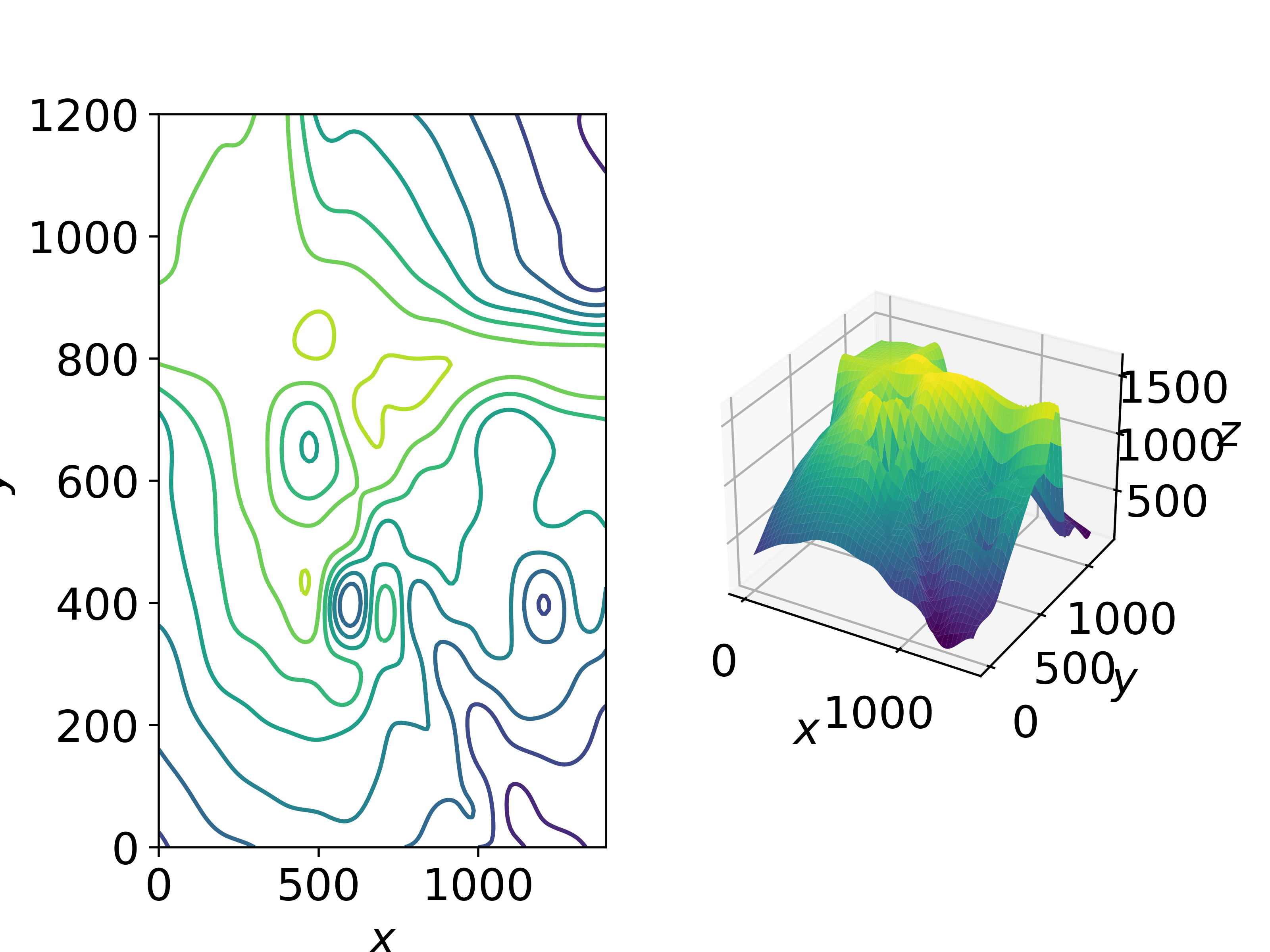
散点插值（griddata）

若数据点并无分布规律，可用griddata进行插值

可处理任意D维的数据点

griddata(points, values, xi, method='linear')

points为数据点位置（D维向量）的序列，values为数据点值的序列

xi为需要插值的空间，形式与points相同，或用格点坐标矩阵的D元组表示

method插值方法：'nearest','linear','cubic'分别对应0，1，3阶插值

返回xi中的数据值

from mpl_toolkits import mplot3d
import matplotlib.pyplot as plt
import numpy as np
from scipy.interpolate import griddata
x = np.array([129, 140, 103.5, 88, 185.5, 195, 105,
              157.5, 107.5, 77, 81, 162, 162, 117.5])
y = np.array([7.5, 141.5, 23, 147, 22.5, 137.5, 85.5, -
              6.5, -81, 3, 56.5, -66.5, 84, -33.5])
z = -np.array([4, 8, 6, 8, 6, 8, 8, 9, 9, 8, 8, 9, 4, 9])
xy = np.array([x, y]).T
xn = np.linspace(x.min(), x.max(), 100)
yn = np.linspace(y.min(), y.max(), 100)
X, Y = np.meshgrid(xn, yn)
zn = griddata(xy, z, (X, Y), method='nearest')
ax = plt.subplot(121, projection='3d')
ax.plot_surface(X, Y, zn, cmap='viridis')
ax.set_xlabel('$x$'), ax.set_ylabel('$y$'), ax.set_zlabel('$z$')
plt.subplot(122)
a = plt.contourf(X, Y, zn, 8, cmap=plt.cm.Spectral)
plt.clabel(plt.contour(xn, yn, zn))
plt.colorbar(a)
plt.savefig('griddata.png', dpi=500), plt.show()