Python使用Matplotlib作图

Matplotlib.pyplot将原本面向对象的作图操作封装成函数，使之更近似于MATLAB的交互式命令

只要有离散的数据，就可以做出柱状、散点、饼状、折线、3D图形等可视化图表

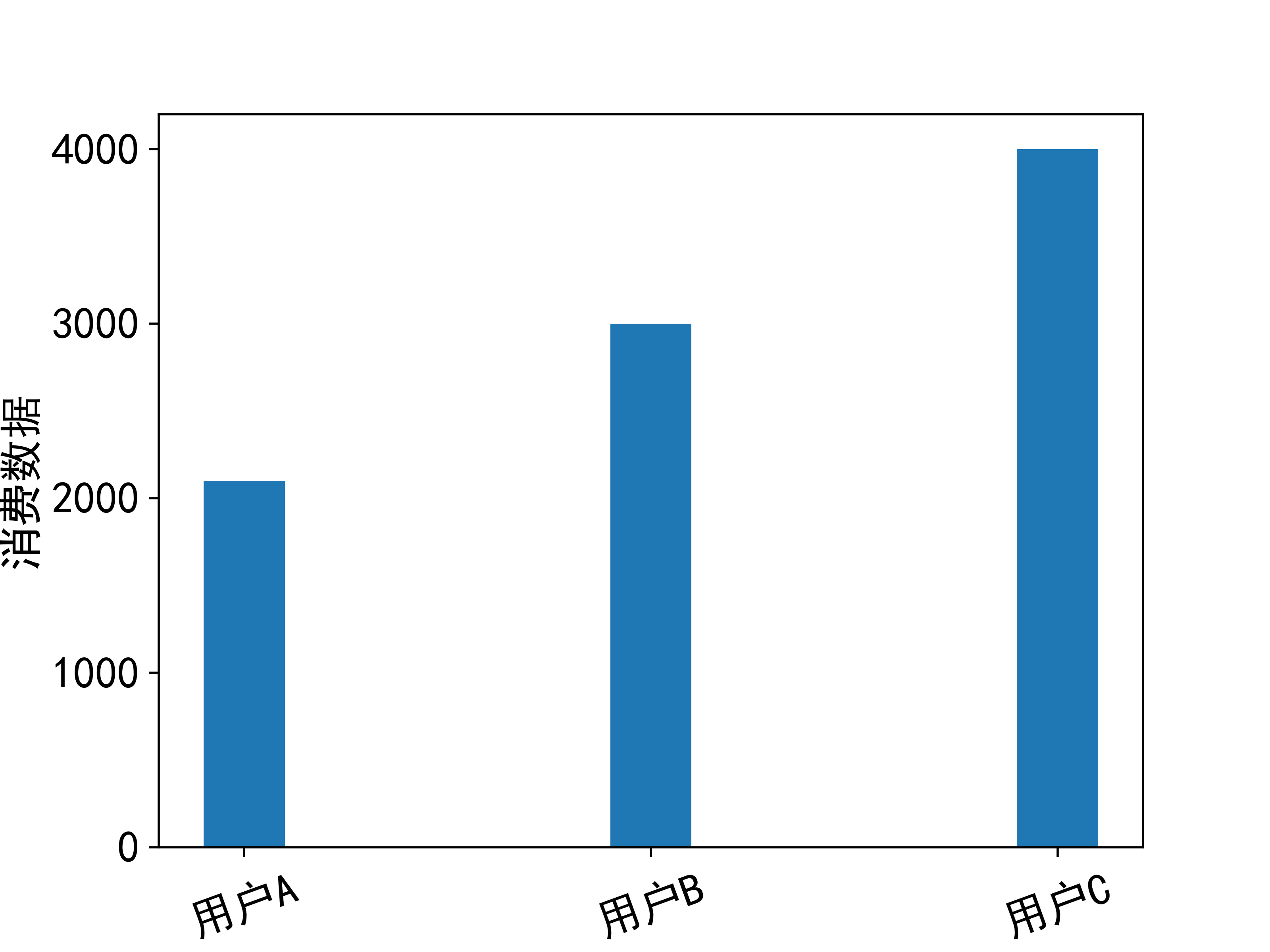
柱状图（bar）

pyplot.bar()只需提供两个数组作为各数据的横纵坐标，即可生成柱状图

from matplotlib import rcParams
from matplotlib.pyplot import *
import numpy as np
y = np.array((2100, 3000, 4000))
x = np.array([1, 2, 3])
width = 0.2
rc('font', size=16)
bar(x, y, width)  # 指定柱宽
ylabel("消费数据")
xticks(x, ["用户A", "用户B", "用户C"], rotation=20)  # 将x标签改为用户名，并旋转20度显示
rcParams['font.sans-serif'] = ['SimHei']  # 设置中文字体，否则会乱码
savefig('bar.png', dpi=500)
show()  # 显示在屏幕

效果图：

若要显示负号，需rcParams['axes.unicode_minus']=False

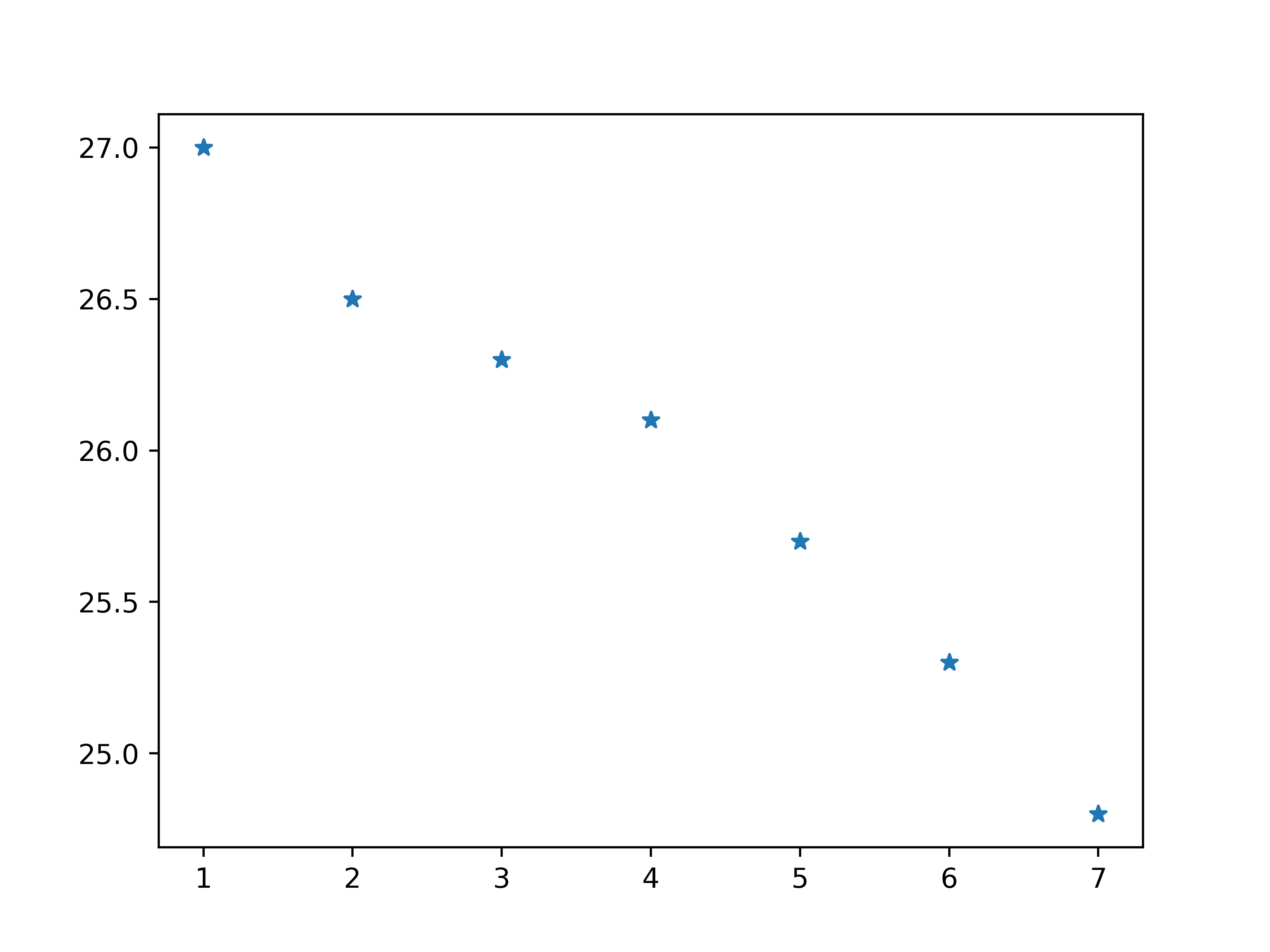
散点图（scatter）

与bar类似

from numpy.linalg.linalg import _eigvalsh_dispatcher
from pylab import *  # pylab=pyplot+部分numpy函数
x = array(range(1, 8))
y = "27.0  26.5 26.3  26.1    25.7 25.3   24.8"
y = ",".join(y.split())
y = array(eval(y))
scatter(x, y, marker='*')  # 用星形显示散点
savefig("scatter.png", dpi=500)
show()

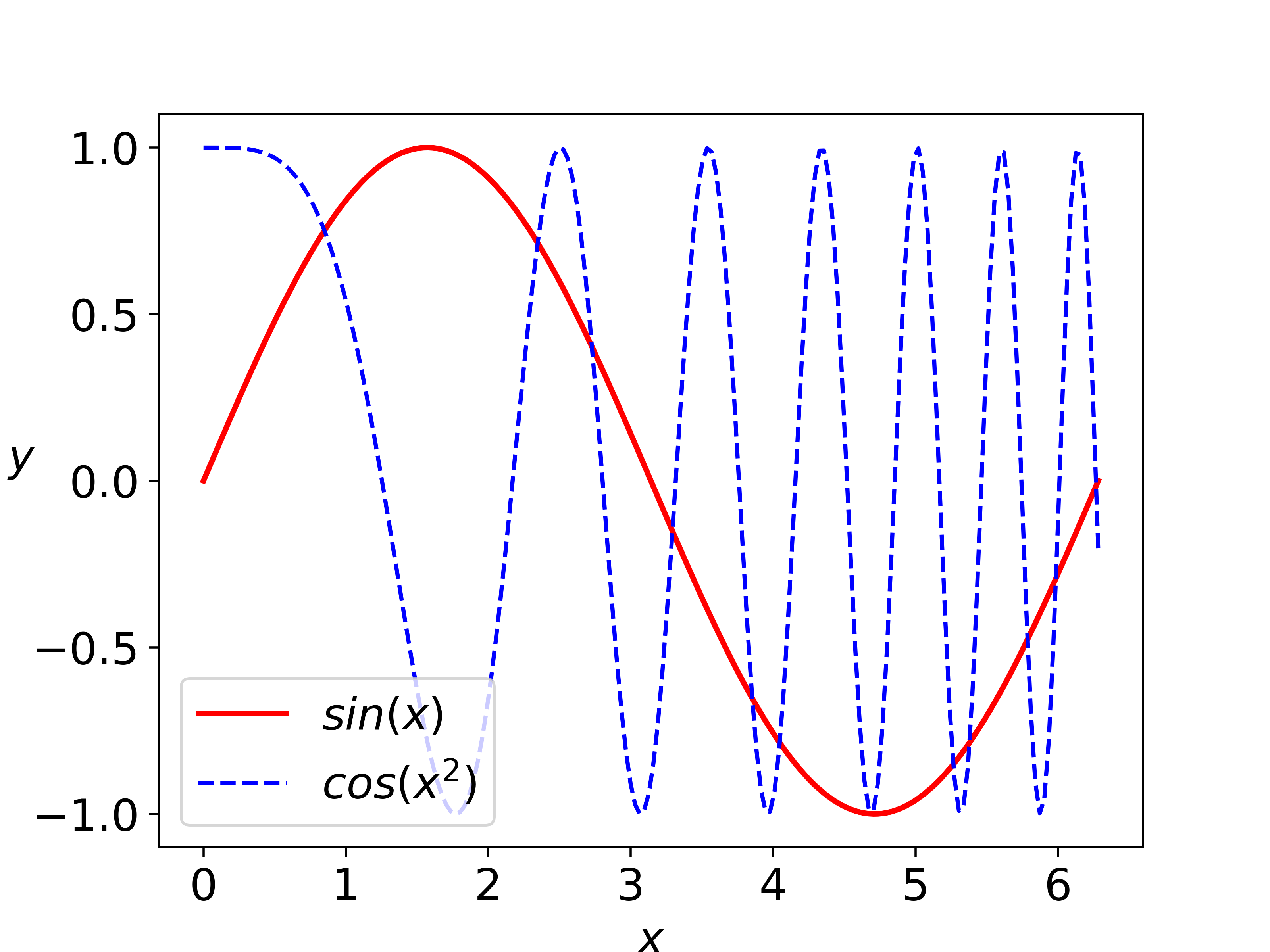
折线图（plot）

基本用法为plot(x,y,s)，前两个参数为数据点的横纵坐标，s为指定线条颜色、线条样式和数据点形状的字符串

也可在同一个坐标内显示多个折线

import numpy as np
from matplotlib.pyplot import *
x = np.linspace(0, 2*np.pi, 200)
y1 = np.sin(x)
y2 = np.cos(pow(x, 2))
rc('font', size=16)
# rc('text', usetex=True) # 可以用LaTeX字体显示
plot(x, y1, 'r-', label='$sin(x)$', linewidth=2)  # 红色实线
plot(x, y2, 'b--', label='$cos(x^2)$')  # 蓝色虚线
xlabel('$x$')
ylabel('$y$', rotation=0)  # y标签默认旋转90度
rc('legend', loc='lower left')  # 图例在左下显示
legend()
savefig('plot.png', dpi=500)
show()

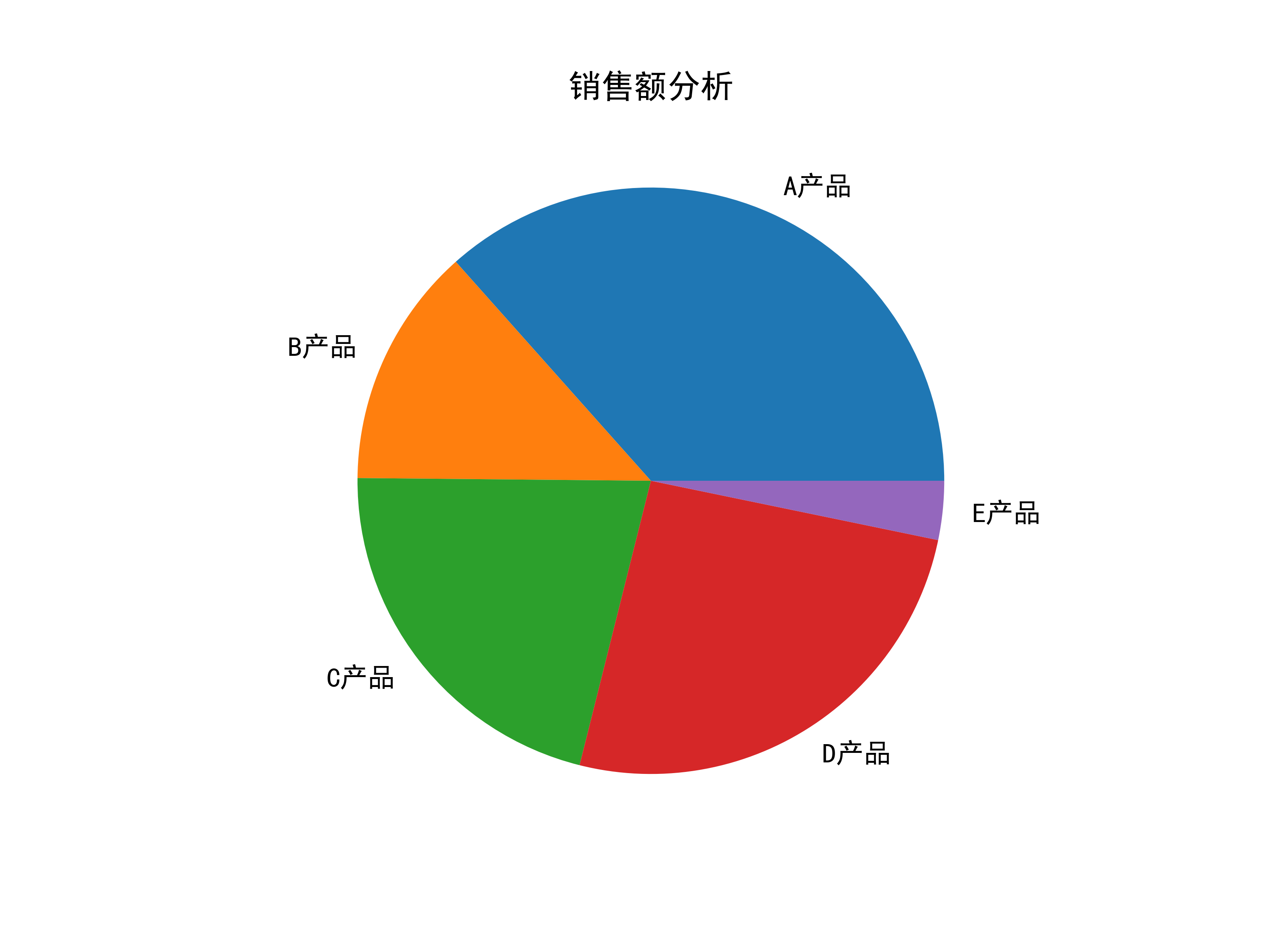
饼状图（pie）

只需一维数组

from matplotlib import rcParams
import numpy as np
from matplotlib.pyplot import *
a = np.array([124, 45, 72, 87, 11])
pie(a, labels=["A产品", "B产品", "C产品", "D产品", "E产品"])
title("销售额分析")
rcParams['font.sans-serif'] = ['SimHei']
savefig("pie.png", dpi=500)
show()

子窗口（subplot）

subplot(nrows, ncols, index)

前两个参数将整个窗口分为nrows*ncols的区域

函数返回从上到下，从左到右的第index个区域（从1开始）

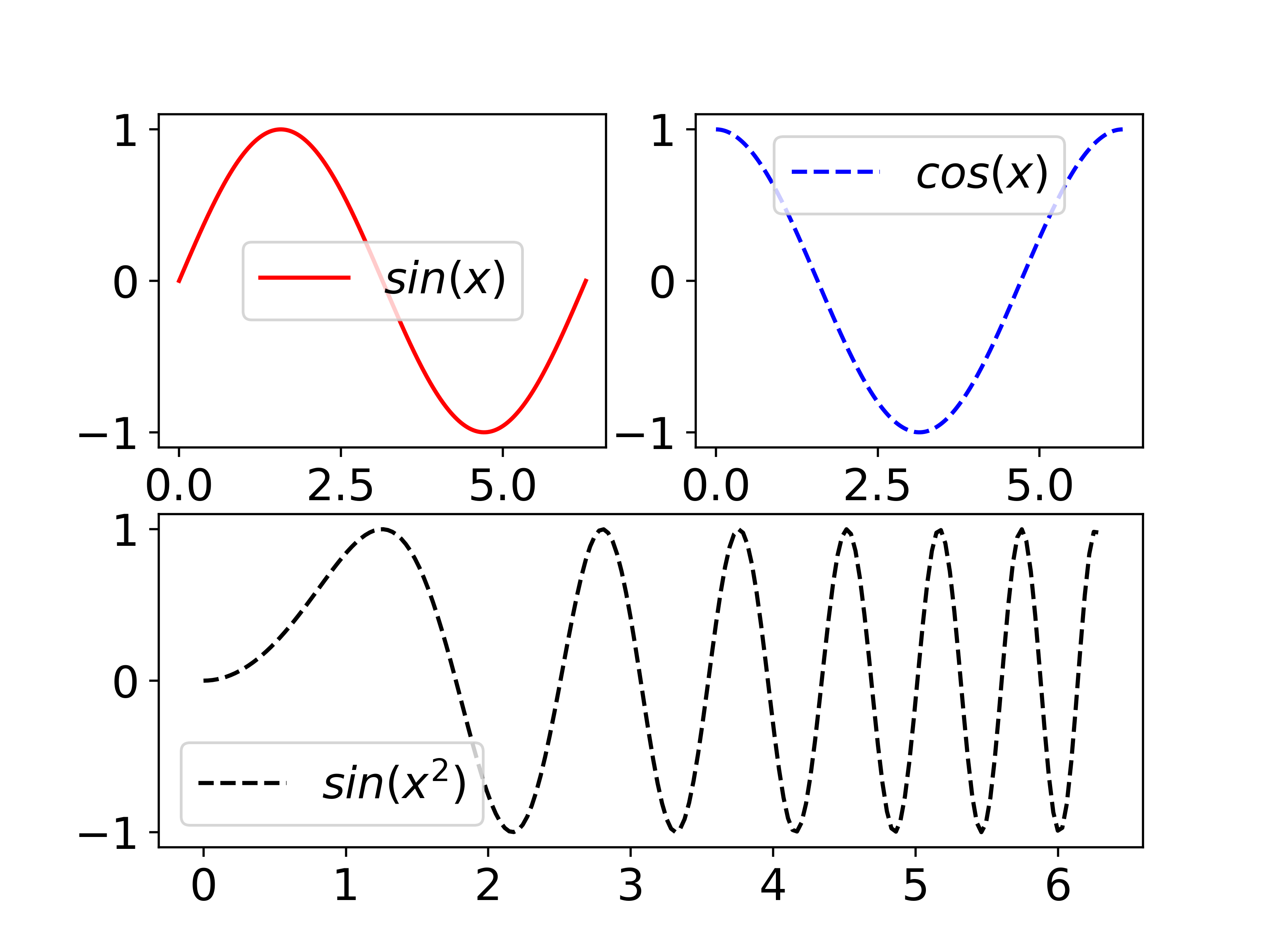
import numpy as np
from matplotlib.pyplot import *
x = np.linspace(0, 2*np.pi, 200)
y1 = np.sin(x)
y2 = np.cos(x)
y3 = np.sin(x*x)
rc('font', size=16)
ax1 = subplot(2, 2, 1)  # 创建左上窗口
ax1.plot(x, y1, 'r', label='$sin(x)$')
legend()

ax2 = subplot(2, 2, 2)  # 创建右上窗口
ax2.plot(x, y2, 'b--', label='$cos(x)$')
legend()

ax3 = subplot(2, 1, 2)  # 创建下方窗口
ax3.plot(x, y3, 'k--', label='$sin(x^2)$')
legend()
savefig('subplot.png', dpi=500)
show()

上方的两个窗口分别占据了2*2划分的前两个区域

下方窗口占据了2*1划分的第二个区域

三维曲线（plot3D）

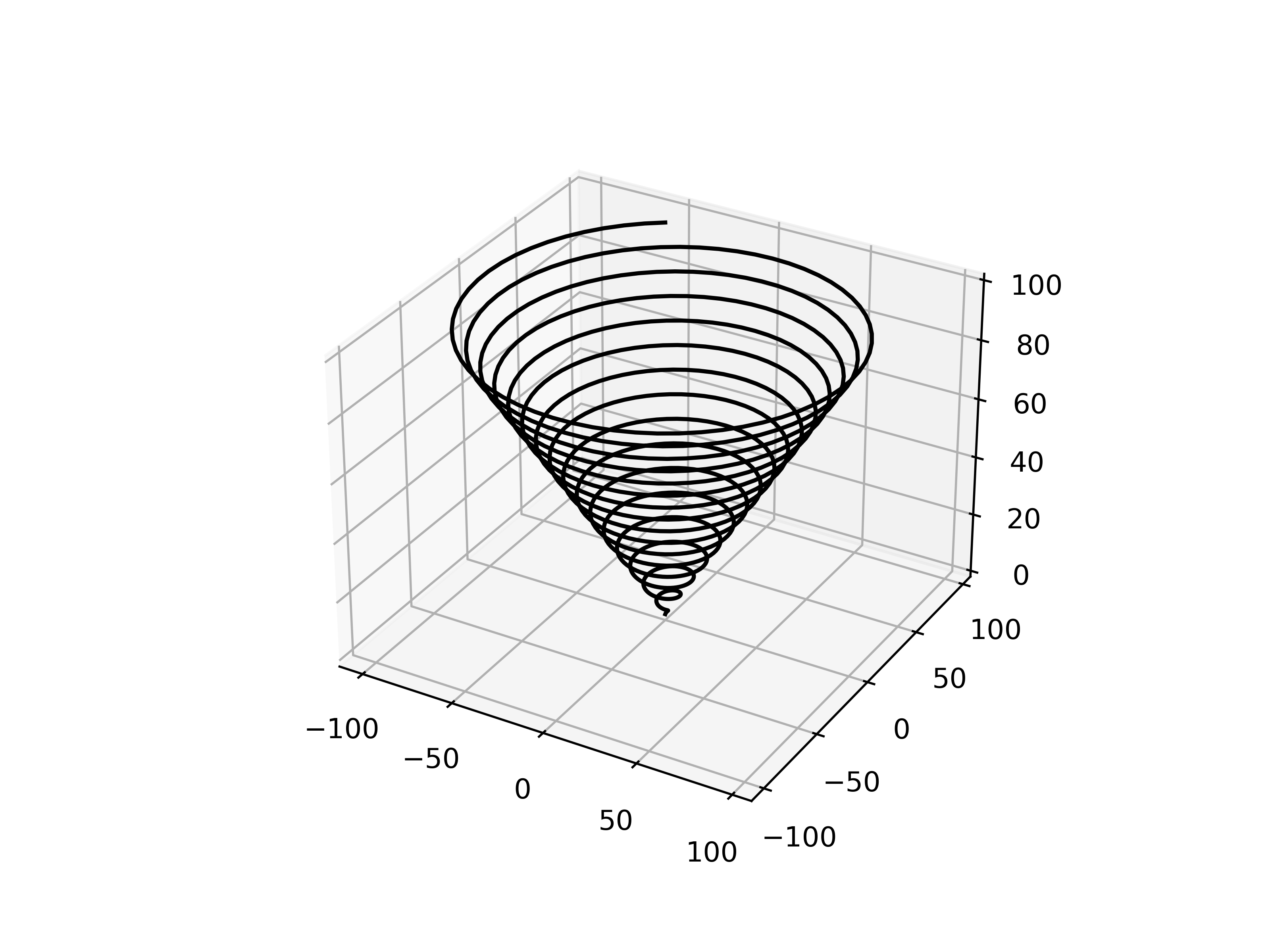
以下代码画出\(x=t\sin t,y=t\cos t,z=t\)的图形

from matplotlib.pyplot import *
import numpy as np
ax = axes(projection='3d')  # 先设置三维模式
z = np.linspace(0, 100, 1000)
x = np.sin(z)*z
y = np.cos(z)*z
ax.plot3D(x, y, z, 'k')
savefig('plot3D.png', dpi=500)
show()

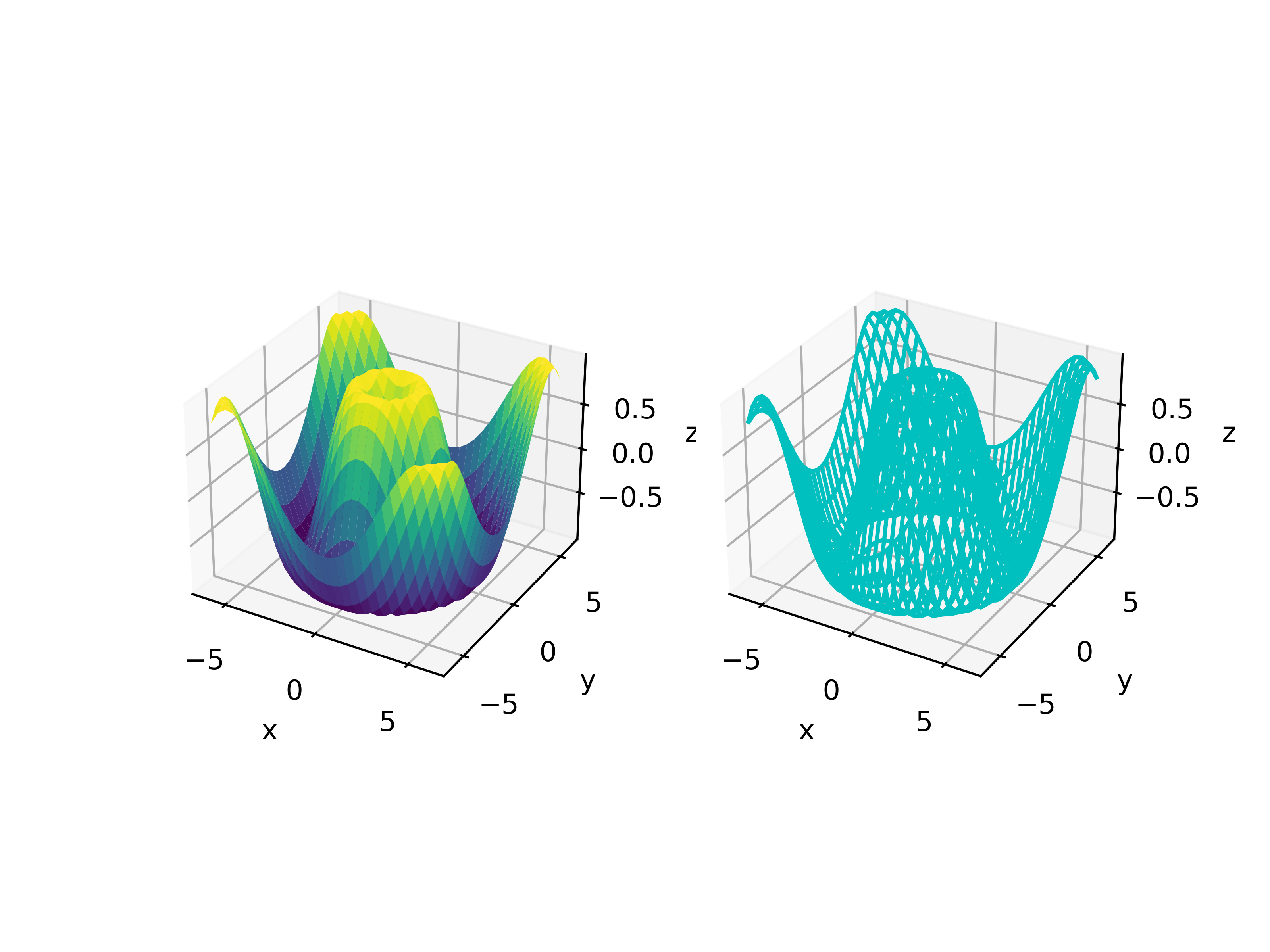
三维曲面（plot_surface,plot_wireframe）

plot_surface生成表面图形，plot_wireframe生成网格图形

生成三维曲面时，需指定网格坐标（描点坐标）

以下代码画出\(z=\sin (\sqrt{x^2+y^2})\)的图形

from matplotlib.pyplot import *
import numpy as np
x = np.linspace(-6, 6, 30)
y = np.linspace(-6, 6, 30)
X, Y = np.meshgrid(x, y)  # 生成网格坐标矩阵
Z = np.sin(np.sqrt(X**2+Y**2))

ax1 = subplot(1, 2, 1, projection='3d')
ax1.plot_surface(X, Y, Z, cmap='viridis')  # 使用viridis的配色创建表面图形
ax1.set_xlabel('x')
ax1.set_ylabel('y')
ax1.set_zlabel('z')

ax2 = subplot(1, 2, 2, projection='3d')
ax2.plot_wireframe(X, Y, Z, color='c')
ax2.set_xlabel('x')
ax2.set_ylabel('y')
ax2.set_zlabel('z')

savefig('plot_surface.png', dpi=500)
show()

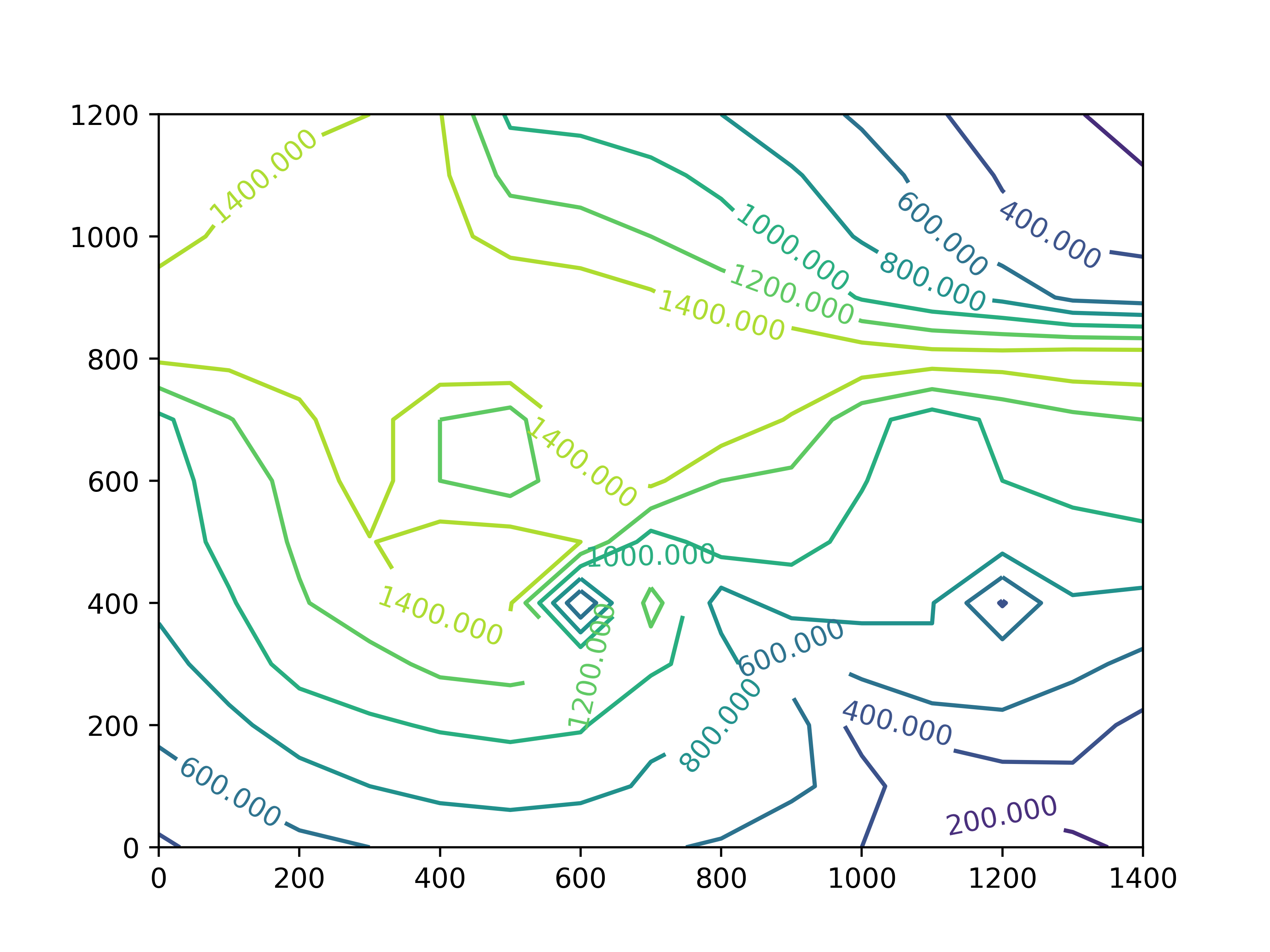
等高线图（contour）

from matplotlib.pyplot import *
import numpy as np
z = np.loadtxt("data.txt") # 从文件导入高程数据
x = np.arange(0, 1500, 100)
y = np.arange(1200, -10, -100)
contr = contour(x, y, z)
clabel(contr) # 标注高度
savefig('contour.png', dpi=500)
show()

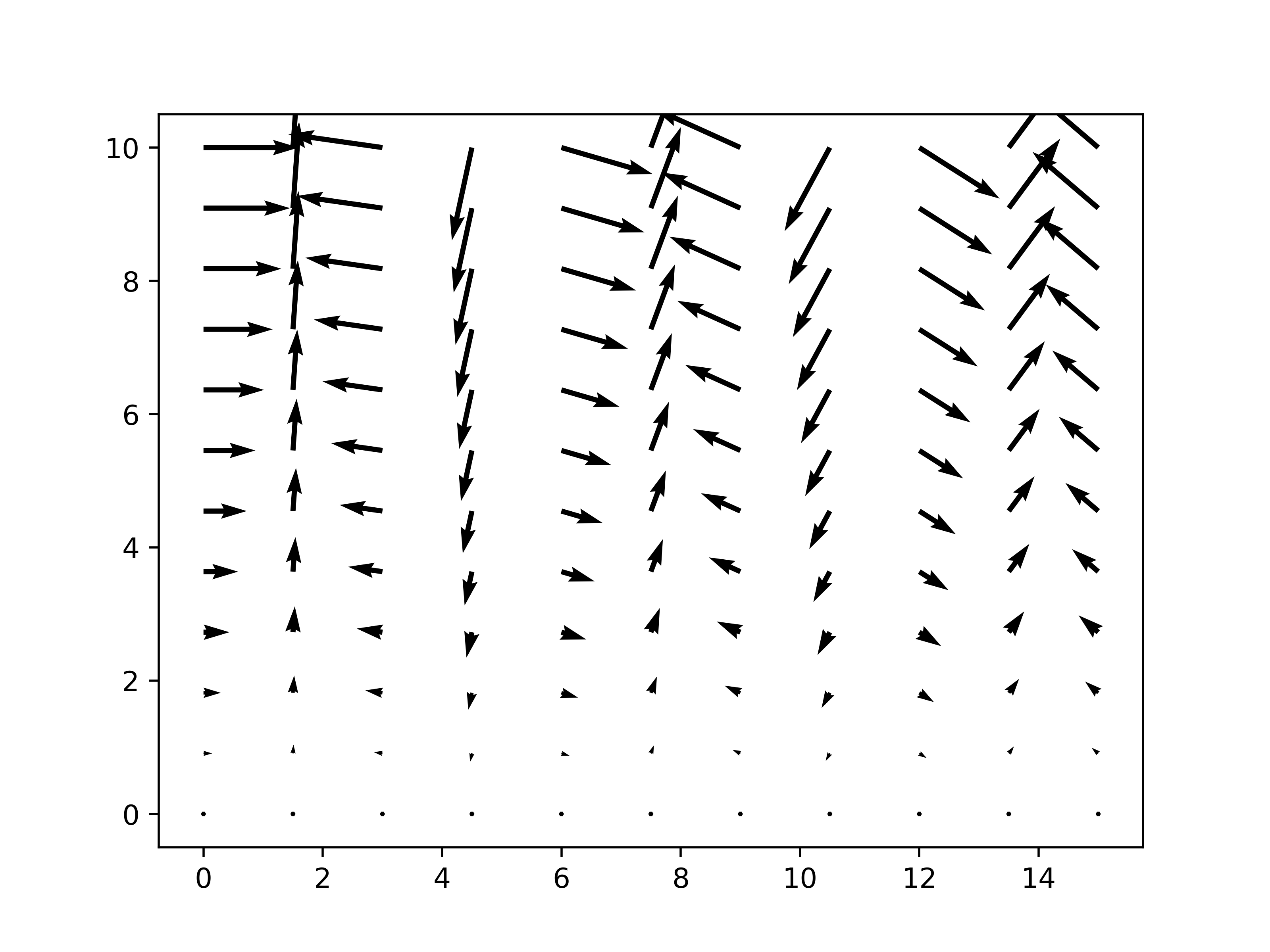
向量图（quiver）

以下代码画出向量场\(\vec A=(y\cos x,y\sin x)\)

quiver(x, y, vx, vy)分别接收两个网格坐标矩阵，以及向量场的xy分量

from matplotlib.pyplot import *
import numpy as np
x = np.linspace(0, 15, 11)
y = np.linspace(0, 10, 12)
x, y = np.meshgrid(x, y)
vx = y*np.cos(x)
vy = y*np.sin(x)
quiver(x, y, vx, vy)
savefig('quiver.png', dpi=500)
show()