Python实现拟合

拟合：给定\(n\)个数据点，求一\(f(x)\)使其与数据点最“接近”，即： \[ J=\sum_{i=1}^n(fx_i-y_i)^2 \] 最小，称为最小二乘拟合。

往往需要提前指定\(f(x)\)的类型，常用的有某次多项式、双曲函数、指数函数等

scipy.optimize.curve_fit可以实现任意类型函数的拟合

用法：

curve_fit(f, xdata, ydata, p0=None)

• f为一函数：f(x,...)，x为自变量，后面的参数全为拟合函数的待定参数
• xdata和ydata是数据点的坐标向量
• p0为待定参数的初值向量
• D维情形，x是D维向量，xdata是D维向量构成的序列，p0同

返回二元组(popt,pcov)：

• popt：一维数组，表示拟合函数的参数
• pcov：二维阵列，popt的估计协方差。对角线提供参数估计的方差。

示例：

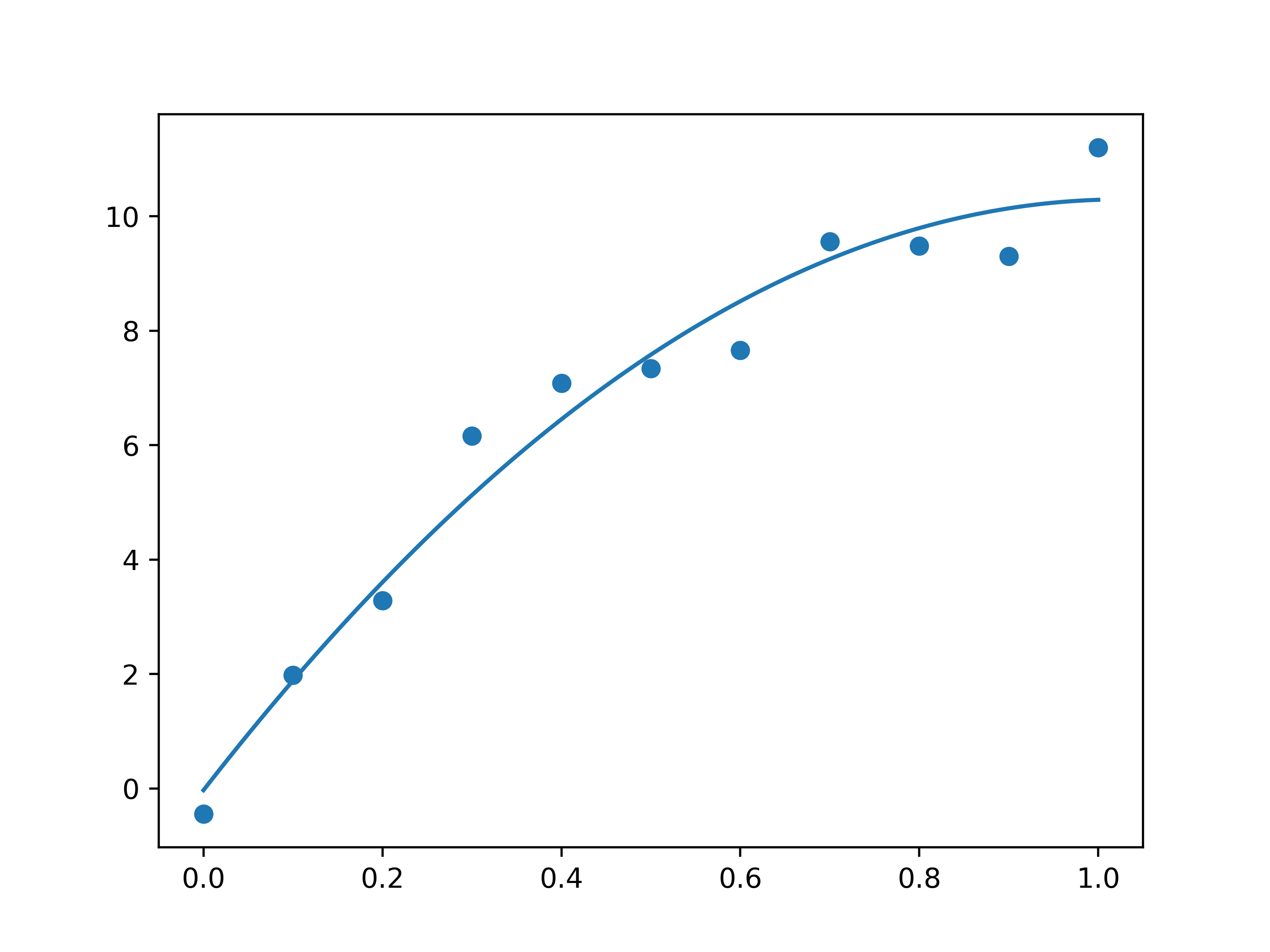
用二次多项式拟合一元函数

import numpy as np
from scipy.optimize import curve_fit
import pylab as plt


def f(x, a, b, c): return a*x**2+b*x+c


x = np.arange(0, 1.1, 0.1)
y = np.array([-0.447, 1.978, 3.28, 6.16, 7.08,
              7.34, 7.66, 9.56, 9.48, 9.30, 11.2])
popt, pcov = curve_fit(f, x, y)
print("a={},    b={},   c={}".format(*popt))  # 打印参数
print("f(0.25)={},f(0.35)={}".format(
    *f(np.array([0.25, 0.35]), *popt)))  # 打印预测值
plt.scatter(x, y)
xn = np.linspace(0, 1, 100)
yn = f(xn, *popt)
plt.plot(xn, yn)
plt.savefig('1.png', dpi=500), plt.show()

输出：

a=-9.810839009366013,    b=20.129292913034863,   c=-0.03167107877459929
f(0.25)=4.387474711398741,f(0.35)=5.811753662140266

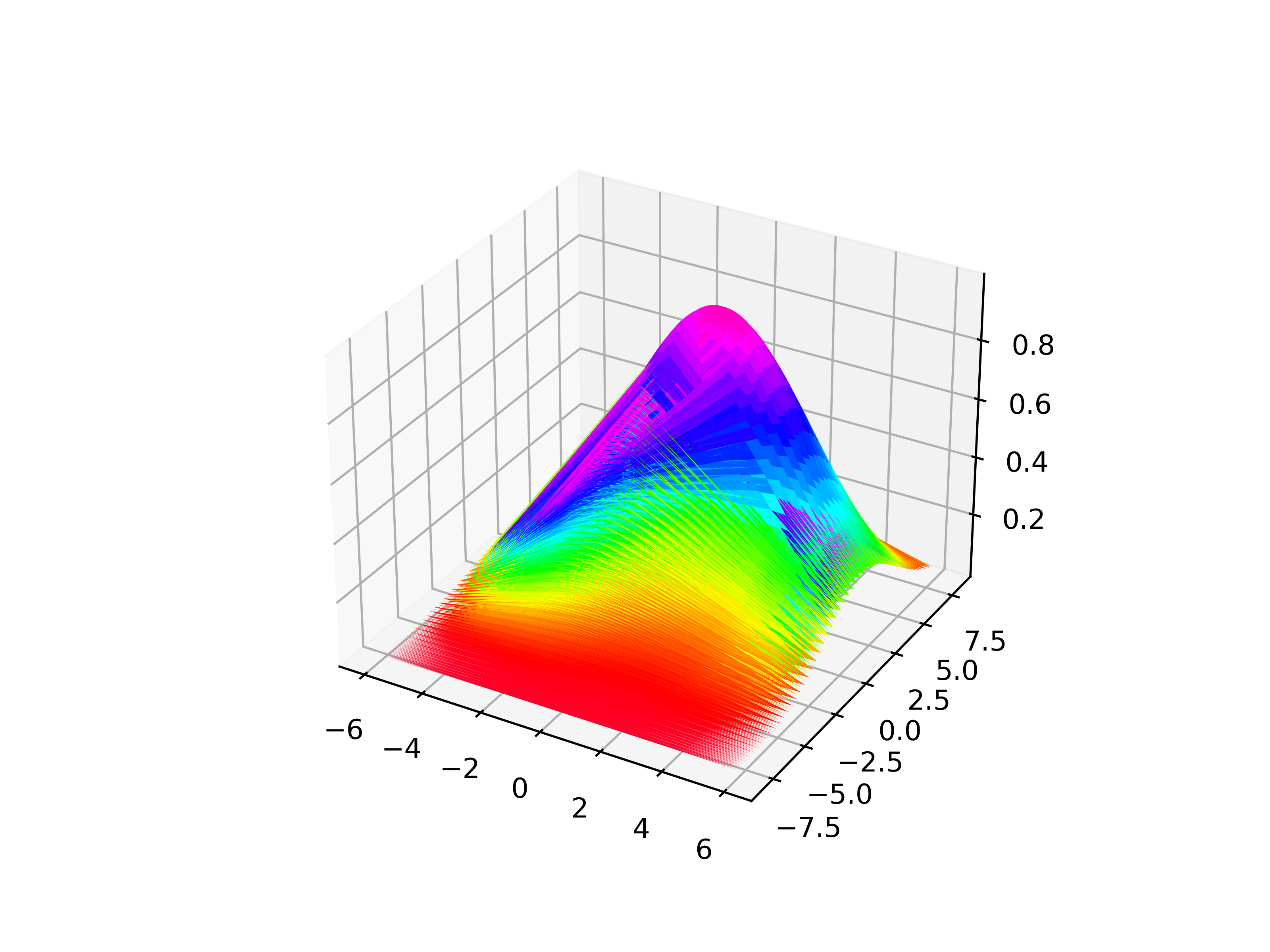
对曲面\(z=e^{-\frac{(x-\mu_1)^2+(y-\mu_2)^2}{2\sigma^2}}\)添加噪声，再进行拟合，其中\(\mu_1=1,\mu_2=2,\sigma=3\)

import numpy as np
from scipy.optimize import curve_fit
import pylab as plt


def f(x, u1, u2, sgm):
    return np.exp(-((x[0]-u1)**2+(x[1]-u2)**2)/(2*sgm**2))


x = np.linspace(-6, 6, 200)
y = np.linspace(-8, 8, 300)
X, Y = np.meshgrid(x, y)  # 获得网格坐标矩阵
X = np.reshape(X, (1, -1))
Y = np.reshape(Y, (1, -1))  # 降维
xy = np.vstack((X, Y))  # 转换成坐标点序列的形式
z = f(xy, 1, 2, 3)  # 求原始函数的各点值
zr = z+0.2*np.random.normal(size=z.shape)  # 生成噪声数据
popt, pcov = curve_fit(f, xy, zr)
print("u1={},    u2={},   sgm={}".format(*popt))  # 打印参数
zn = f(xy, *popt)  # 求拟合函数的各点值
X = np.reshape(X, (200, 300))
Y = np.reshape(Y, (200, 300))
zn = np.reshape(zn, (200, 300))
ax = plt.axes(projection='3d')
ax.plot_surface(X, Y, zn, cmap='gist_rainbow')
plt.savefig('2.png', dpi=500), plt.show()

输出：

u1=1.0055785483402968,    u2=2.002582704331591,   sgm=3.0134682873777496