求导
scipy.misc.derivative可用于求任意函数的任意阶导数:
def derivative(func, x0, dx=1.0, n=1, order=3)
func:自定义的被求导函数\(f(x)\) x0:求导的位置,即求\(f^{(n)}(x_0)\) dx:用于微分的小量n:求导的阶数order:用于求导的采样点个数,必须为>=n+1的奇数
示例:
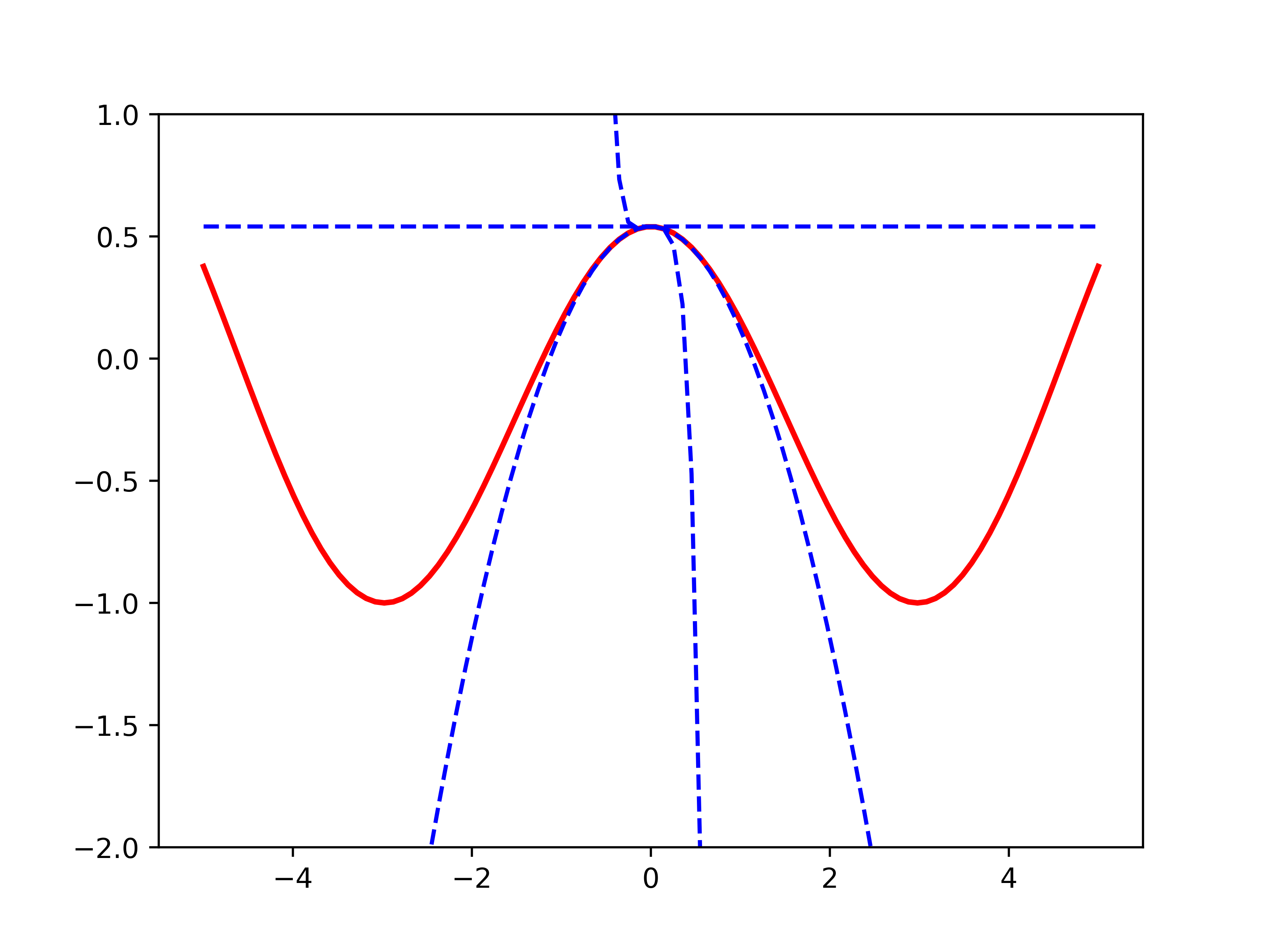
画出\(\cos\sqrt{x^2+1}\) 及其在\(0\) 点处的\(1,3,5\) 阶泰勒展开式 \[
f(x)=f(x_0)+f'(x_0)(x-x_0)+\frac{f''(x_0)}{2!}(x-x_0)^2+\dots+\frac{f^{(i)}(x_0)}{i!}(x-x_0)^i+\dots
\]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 import numpy as npfrom scipy.misc import derivativeimport pylab as pltdef f (x) : return np.cos(np.sqrt(x**2 +1 )) def fac (x) : if (x <= 1 ): return 1 return fac(x-1 )*x dx = 1e-4 x = np.linspace(-5 , 5 , 100 ) y = f(x) plt.plot(x, y, 'r-' , linewidth=2 ) now = f(np.zeros(100 )) for i in range(1 , 6 ): now += derivative(f, 0 , dx, i, order=7 )*(x**i)/fac(i) if (i in [1 , 3 , 5 ]): plt.plot(x, now, 'b--' ) plt.ylim((-2 , 1 )) plt.savefig("derivative.png" , dpi=500 ) plt.show()
定积分
一重积分
scipy.integrate.quad可以求任意函数的一重积分
quad(func, a, b)表示求函数func从a到b的一重积分
示例:
求\(\int_0^\infty e^{-x}\sin(x^2+2)\)
1 2 3 4 5 6 7 8 9 import numpy as npfrom scipy.integrate import quaddef f (x) : return np.exp(-x)*np.sin(x**2 +2 ) print(quad(f, 0 , np.inf))
输出:
1 (0.37378979243874044, 1.3876530327162045e-08)
返回的值分别是积分结果和绝对误差
多重积分
scipy.integrate.dblquad和scipy.integrate.tplquad分别能够求二重和三重积分
dblquad(func,a,b,gfun,hfun)表示\(\int_a^b \text dx \int_{gfun(x)}^{hfun(x)} func(x,y) \text dy\)
tplquad(func,a,b,gfun,hfun,qfun,rfun)表示\(\int_a^b \text dx \int_{gfun(x)}^{hfun(x)} \text dy \int_{qfun(x,y)}^{rfun(x,y)} func(x,y,z) \text dz\)
返回值和quad一致
需要注意的是,func定义的参数顺序必须是func(x,y,z)
非线性方程(组)
scipy.optimize.fsolve可以解非线性方程(组)
fsolve(func,x0)表示求\(func(x)=0\) 的根,迭代初值x0
若要解方程组,可将func(x)的x定义为向量
示例: \[
x^3+1.1x^2+0.9x-1.4=0 \\
\begin{cases}
5x_2+3=0 \\
4x_1^2-2\sin(x_2x_3)=0 \\
x_2x_3-1.5=0
\end{cases}
\]
1 2 3 4 5 6 7 8 9 10 11 12 import numpy as npfrom scipy.optimize import fsolveprint(fsolve(lambda x: x**3 +1.1 *x**2 +0.9 *x-1.4 , 0 )) def f (x) : x1, x2, x3 = x.tolist() return [5 *x2+3 , 4 *x1**2 - 2 *np.sin(x2*x3), x2*x3 - 1.5 ] print(fsolve(f, [1 , 1 , 1 ]))
输出:
1 2 [0.67065731] [-0.70622057 -0.6 -2.5 ]
求极值点
scipy.optimize.minimize是求非线性规划的函数,若不加约束,即可求任意函数(一元,多元)的极小值点
minimize(func,x0)表示求\(func(x)=0\) 的最小值,迭代初值x0
返回的是一个result类,可以调用成员以获取相应信息
示例: \[
f_1(x)=e^x\cos(2x) \\
f_2(x_1,x_2)=100(x_2-x_1^2)^2+(1-x_1)^2
\]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 import numpy as npfrom scipy.optimize import minimizedef f1 (x) : return np.exp(x)*np.cos(2 *x) def f2 (x) : x1, x2 = x.tolist() return 100 *(x2-x1**2 )**2 +(1 -x1)**2 print(minimize(f1, 0 ), '\n' ) print(minimize(f2, [2 , 2 ]))
输出:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 fun: -0.2344426467071059 hess_inv: array([[0.85441485]]) jac: array([-1.86264515e-08]) message: 'Optimization terminated successfully.' nfev: 14 nit: 5 njev: 7 status: 0 success: True x: array([-1.33897255]) fun: 1.8932893809017893e-11 hess_inv: array([[0.51675994, 1.03186494], [1.03186494, 2.0655726 ]]) jac: array([ 5.27380711e-06, -2.50575298e-06]) message: 'Optimization terminated successfully.' nfev: 105 nit: 30 njev: 35 status: 0 success: True x: array([0.99999565, 0.99999129])