SciPy求微分方程数值解

一阶微分方程（组）

scipy.integrate.odeint()可以数值解一阶微分方程（组）

不同于微分方程的符号解，可以给出未知函数的表达式，数值解只能求得指定位置的函数值

sol=odeint(func, y0, t)

• func：表示一个微分方程\(\frac{\text dy}{\text dt} = func(y, t)\)，其中的y可以是向量，以表示微分方程组
• y0：未知函数的初值条件，表示\(y(t[0])=y_0\)，即第一个自变量取值处的函数值，同样可以是向量
• t：自变量的取值序列

返回值sol是一个len(t)*len(y0)的数组，表示每个取值位置的函数值

示例： \[ \begin{cases} y'=-2y+x^2+2x \\ y(1)=2 \end{cases} \] 代码在下面一起给出

高阶微分方程（组）

通过换元可以将高阶微分方程转化为一阶微分方程： \[ y_0=y \\ y_1=y_0'=y' \\ y_2=y_1'=y'' \\ \dots \\ y_k=y_{k-1}'=y^{(k)} \\ \] 这样就同样可以使用odeint()来获得数值解了

示例： \[ \begin{cases} y''+2y'+2y=0 \\ y(0)=0, y'(0)=1 \end{cases} \] 先转化成： \[ \begin{cases} y_0'=y_1 \\ y_1'=-2y_1-2y_0 \\ y_0(0)=0, y_1(0)=1 \end{cases} \]

import numpy as np
from scipy.integrate import odeint
import pylab as plt


def dy(y, x):
    return -2*y+x**2+2*x


x = np.arange(1, 10.5, 0.5)
sol = odeint(dy, 2, x)
print(sol.T)


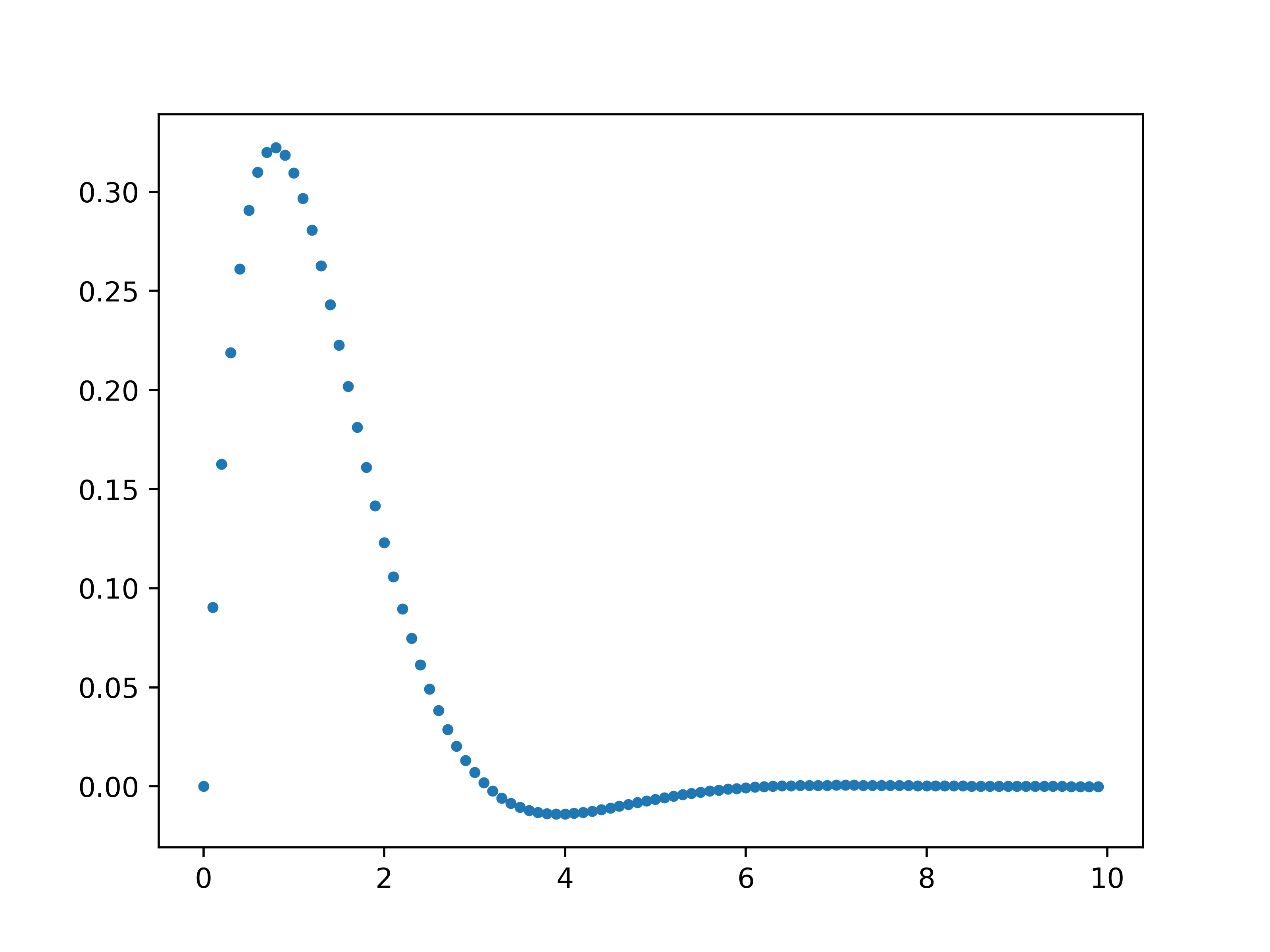
def dy(y, x):
    y0, y1 = y
    return [y1, -2*y1 - 2*y0]


x = np.arange(0, 10, 0.1)
sol = odeint(dy, [0, 1], x)
plt.scatter(x, sol.T[0], marker='.')  # 只需要y的0阶导数据
plt.savefig('odeint.png', dpi=500)
plt.show()

输出：

[[ 2.          2.08484933  2.9191691   4.18723381  5.77289452  7.63342241
   9.75309843 12.12613985 14.75041934 17.62515427 20.75005673 24.12502089
  27.7500077  31.62500278 35.75000104 40.1250004  44.75000015 49.62500006
  54.75000002]]

Lorenz模型的混沌效应

Lorenz方程： \[ \begin{cases} \dot x=\sigma(y-x) \\ \dot y=\rho x-y-xz \\ \dot z=xy-\beta z \end{cases} \] 模拟\(\sigma=10,\rho=28,\beta=\frac 8 3\)时\(t\in [0,50]\)的运行轨迹，以及给初值微小扰动后解的偏差演化曲线

import numpy as np
from scipy.integrate import odeint
import pylab as plt


def lorenz(w, t):
    sigma = 10
    rho = 28
    beta = 8/3
    x, y, z = w
    return [sigma*(y-x), rho*x-y-x*z, x*y-beta*z]


t = np.arange(0, 50, 0.01)
sol1 = odeint(lorenz, [0., 1., 0.], t)
sol2 = odeint(lorenz, [0., 1.0001, 0.], t)

ax1 = plt.subplot(121, projection='3d')
ax1.plot(sol1[:, 0], sol1[:, 1], sol1[:, 2], linewidth=1)
ax2 = plt.subplot(122, projection='3d')
ax2.plot(sol1[:, 0]-sol2[:, 0], sol1[:, 1] -
         sol2[:, 1], sol1[:, 2]-sol2[:, 2], linewidth=1)
plt.savefig('lorenz.png', dpi=500)
plt.show()