一些前置知识:
x=symbols('x')声明变量\(x\)
y.subs(x,x0)\(y\)是\(x\)的表达式时,带入\(x=x_0\)的值
y.n()常量表达式求浮点值
求极限
limit(e, z, z0, dir="+")
\(e\)是\(z\)的表达式,求\(e(z)\)在\(z_0\)处的极限,\(\text{dir}\)可以指定是\(z_0^+\)还是\(z_0^-\)
以下计算了\(\lim_{x\rightarrow 0}\frac{\sin x}x\),\(\lim_{x\rightarrow \infty} (1+\frac 1 x)^x\),\(\lim_{x\rightarrow 0}\sin(\frac 1 x)\)三个极限
1 | from sympy import * |
输出:
1 | 1 |
求导数
diff(expr,x1,n1,x2,n2,...)
表达式expr依次对xi求ni阶偏导,ni不写默认为1
\(z=\sin x+x^2e^y\),求\(\frac{\partial^2 z}{\partial x^2},\frac{\partial z}{\partial y},\frac{\partial^2 z}{\partial x\partial y}\)
1 | from sympy import * |
输出:
1 | 2*exp(y) - sin(x) |
级数求和
summation(expr,(i,a,b))
expr是关于i的函数,求\(\sum_{i=a}^b expr(i)\)
示例:\(\sum_{k=1}^n k^2\)和\(\sum_{k=1}^\infty \frac 1 {k^2}\)
1 | from sympy import * |
输出:
1 | n*(n + 1)*(2*n + 1)/6 |
泰勒展开
series(expr, x=None, x0=0, n=6, dir="+")
\(expr\)是\(x\)的表达式,在\(x_0\)处的\(n\)阶展开,\(\text{dir}\)可以指定是\(x_0^+\)还是\(x_0^-\)
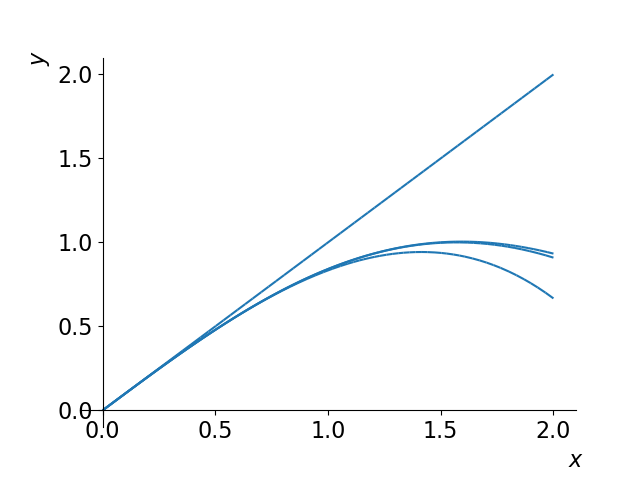
下面演示了\(\sin x\)在0点的3,5,7阶泰勒展开式
1 | from pylab import rc |
输出:
1 | x + O(x**3) |
积分
不定积分:
integrate(f,x)
相当于\(\int f(x)\mathrm d x\)
定积分:
integrate(f,(x,a,b))
相当于\(\int_a^b f(x)\mathrm d x\)
以下代码求解\(\int_0^\pi \sin(2x)\mathrm d x,\int_0^{+\infty} \frac {\sin(x)} x\mathrm d x,\int \sin(x)e^x\mathrm d x\)
1 | from sympy import * |
输出:
1 | 0 |
解代数方程(组)
solve(expr,x)
求解方程\(expr=0\),其中\(x\)是自变量
返回一个list存放所有的根
solve([...,expr_i,...],[...,x_i,...])
求解方程组,其中\(expr_i\)对应\(x_i\)
返回一个list存放所有根,每个根用一个tuple表示,对应此根所有各个变量的值
roots(expr,x)
返回一个dict,表示每个根以及它的重数
示例: \[ x^3-1=0 \\ (x-2)^2(x-1)^3=0 \\ \begin{equation} \begin{cases} x^2+y^2=1 \\ x-y=0 \end{cases} \end{equation} \]
1 | from sympy import * |
输出:
1 | [1, -1/2 - sqrt(3)*I/2, -1/2 + sqrt(3)*I/2] |
微分方程(组)的通解
微分方程中的\(y\)是关于\(x\)的函数,而且是未知函数,而非未知量,因此要将\(y\)声明为Function
y=Function('y')
y=symbols('y',cls=Function)
两种写法都是可以的
dsolve(eq,f(x),ics=),其中eq是关于f(x)的表达式,求解\(eq=0\)
ics可以以一个dict指定f(x)的初值
示例: \[ y''-5y'+6y=0 \\ y''-5y'+6y=xe^{2x} \\ y''-5y'+6y=0,y(0)=1,y'(0)=0 \\ y''-5y'+6y=xe^{2x},y(0)=1,y(2)=0 \]
1 | from sympy import * |
输出:
1 | Eq(y(x), (C1 + C2*exp(x))*exp(2*x)) |


