后缀数组之倍增算法

学习笔记 后缀数组 评论

后缀数组（Suffix Array,SA）可以通过预处理文本串，解决多模板匹配问题。

而AC自动机正好相反，需要事先知道所有的模板。

这是需要首先注意的。

后缀数组

定义字符串的后缀的编号为首字母在原串中的位置。

后缀数组的定义：将字符串的所有后缀排序，其编号构成的数组称为后缀数组

相比后缀自动机和后缀树，后缀数组更为简单，所以更为常用

后缀数组的构造

常使用倍增算法构造后缀数组

其思想是名次的大小体现了子串的大小，将两个名次当作二元组排序。

参与排序的子串长度倍增，最终变成全串的后缀

​

首先对所有后缀的第一个字符排序：（图片来自网络）

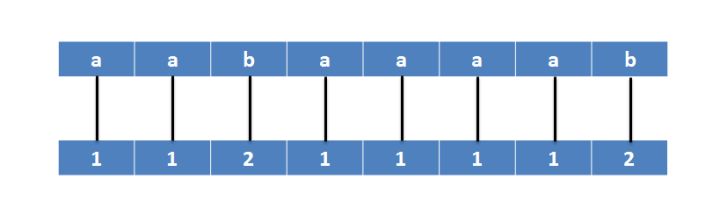
将得到的名次两两绑定再排序：

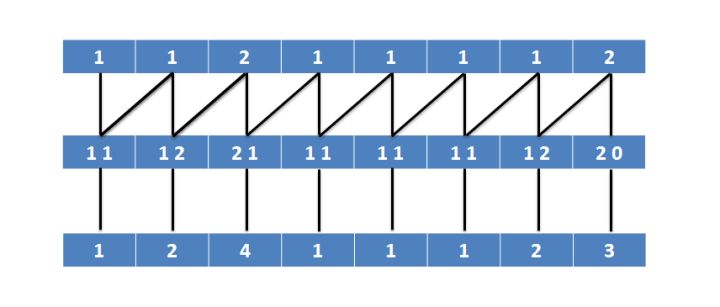
得到的名次再排序:

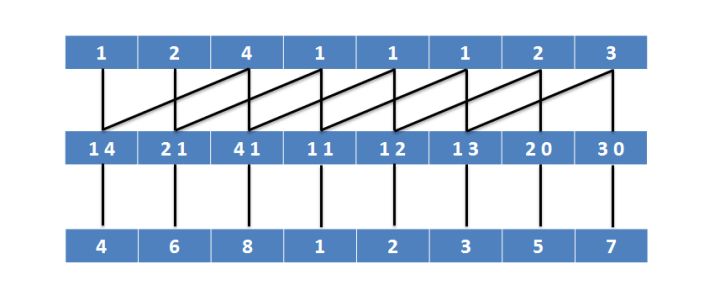
此时每个元素已经代表4个后缀了，依次类推便可将所有后缀排序，排名不变动表示排序已完成

这样倍增的次数是\(O(logn)\)的，如果每次使用基数排序，复杂度为\(O(nlogn)\)

还是比较强大的。

这里提供两个模板：

1.用vector模拟基数排序，便于理解但常数大

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
vector<int> buc[maxn];
int rk[maxn*2],res[maxn],id[maxn];
void csort(int k){
	for (int i=0;i<=m;i++) buc[i].clear();
	for (int i=1;i<=n;i++) buc[rk[id[i]+k]].push_back(id[i]);
	id[0]=0;
	for (int i=0;i<=m;i++){
		int len=buc[i].size();
		for (int j=0;j<len;j++) id[++id[0]]=buc[i][j];
	}
}
void make_sa(){
	m=128;
	for (int i=1;i<=n;i++) rk[i]=s[i];
	for (int k=1;k<n;k<<=1){
		for (int i=1;i<=n;i++) id[i]=i;
		csort(k); csort(0);
		id[0]=0; int t=0;
		for (int i=1;i<=n;i++){
			if (!(rk[id[i]]==rk[id[i-1]]&&rk[id[i]+k]==rk[id[i-1]+k])) t++;
			res[id[i]]=t;
		}
		for (int i=1;i<=n;i++) rk[i]=res[i];
		if (t>=n) break;
		m=t;
	}
	for (int i=1;i<=n;i++) sa[rk[i]]=i;
}

2.每次倍增都更新SA，通过叠加得到名次

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
int rk[maxn],t[maxn],buc[maxn];
void get_sa(){
	cl(buc,0);
	for (int i=1;i<=n;i++) buc[rk[t[i]]]++;
	for (int i=1;i<=m;i++) buc[i]+=buc[i-1];
	for (int i=n;i>=1;i--) sa[buc[rk[t[i]]]--]=t[i];
}
void make_sa(){
	m=128;
	for (int i=1;i<=n;i++) rk[i]=s[i],t[i]=i;
	get_sa();
	for (int k=1;k<n;k<<=1){
		int p=0;
		for (int i=n-k+1;i<=n;i++) t[++p]=i;
		for (int i=1;i<=n;i++) if (sa[i]>k) t[++p]=sa[i]-k;
		get_sa(); t[sa[1]]=p=1;
		for (int i=2;i<=n;i++)
		 if (rk[sa[i]]==rk[sa[i-1]]&&rk[sa[i]+k]==rk[sa[i-1]+k]) t[sa[i]]=p;else t[sa[i]]=++p;
		memcpy(rk,t,sizeof(t));
		if (p==n) break;
		m=p;
	}
}

后缀数组的应用

多模板匹配

由于已经得到了所有后缀的排序，可以直接二分，验证这个后缀是否比模板串大

如果模板串是一个后缀的前缀，就说明模板串是文本串的子串，二分得到的上下界一减就知道匹配了几次

时间复杂度\(O(mlogn)\)，m是模板串长度

求LCP

设\(height[i]\)表示串\(sa[i]\)与串\(sa[i-1]\)的LCP

那么\(sa[i]\)与\(sa[j]\)两个后缀的LCP就等于\(\mathop{Max} \limits^j_{k=i+1}\{ height[sa[k]] \}\)

其实求LCP就转化为RMQ问题了

如何求\(height\)呢？

令\(h[i]=height[rank[i]]\)

那么就有这样一个性质： \[ h[i]\ge h[i-1]-1 \]

证明如下：

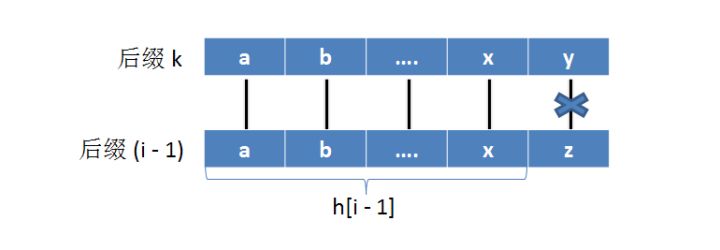
设\(rank[k]=rank[i-1]-1\)，则\(h[i-1]=LCP\{i-1,k\}\)

那么将这两个后缀去掉第一个字符，得到后缀\(k+1\)和\(i\)

其实\(h[i-1]-1=LCP\{k+1,i\}\)，而此时\(rank[k+1]\le rank[i]-1\)

所以\(h[i]\ge h[i-1]-1\)

利用这个性质，每次用\(h[i-1]\)就可以推出\(h[i]\)，再得到\(height[i]\)，复杂度\(O(n)\)

代码如下，很简单：

1
2
3
4
5
6
for (int i=1,h=0;i<=n;i++){
	if (h) h--;
	int j=sa[rk[i]-1];
	while (s[i+h]==s[j+h]) h++;
	ht[rk[i]]=h;
}

求第K大子串

考虑后缀\(sa[i]\)能够提供\(n-sa[i]+1-height[i]\)个本质不同的子串

用二分看第K个子串落在哪个后缀中就好了

​

相同子串算多个：

这个只能\(O(nlogn)\)回答了，BZOJ3998

二分这个子串是哪个后缀的前缀

只要知道有多少子串比当前后缀小即可

排名更前的任意子串都比它小，贡献\(\sum n-sa[i]+1\)

排名更后的其实就是LCP会比它小，贡献\(\sum_i LCP(sa[i],sa[mid])\)

求子串Rank

直接二分找到第一个含该子串的后缀，然后

求\(n-sa[i]+1-height[i]\)的前缀和，就能得到比该子串小的个数了

子串是哪些后缀的前缀

显然答案是一个连续的区间（rank连续）

假设求子串\(S_{a,b}\)，首先得到\(rank[a]\)，答案就是向两边扩展一下

可以发现答案区间内所有后缀与后缀a的LCP一定大于等于\(b-a+1\)

预处理关于\(height\)的ST表，直接倍增一下得到这个区间

子串是否包含另一个子串

假设询问子串\(S_{a,b}\)是否包含子串\(S_{c,d}\)

可以知道子串\(S_{c,d}\)是哪些后缀的前缀，这些后缀的排名是连续的

只要出现某个后缀的开头属于\([a,b-(d-c+1)+1]\)就有了

相当于在区间内询问是否有值属于某区间，主席树维护就好了

​

暂时先写这么多，想到再补……

linkfqyA link to the past.

咸鱼一条